Үнэний вектор ашиглан функцийг тодорхойлох. Бүрэн хоёртын мод ашиглахыг зааж өгөх скаляр аргументийн вектор функц

Скаляр аргументийн вектор функцийн утгуудын багцыг 0 цэгт нийтлэг эх болгон бууруулъя. Декартын координатын системийн эхийг энэ цэгтэй тааруулъя. Дараа нь дурын векторыг нэгж вектор болгон өргөжүүлж болно

Тиймээс скаляр аргументийн вектор функцийг зааж өгнө гэдэг нь гурван скаляр функцийг зааж өгнө гэсэн үг юм Аргументийн утга өөрчлөгдөхөд векторын төгсгөл нь орон зай дахь муруйг дүрслэх бөгөөд үүнийг вектор ходограф гэж нэрлэдэг.

Ойрын үнэ цэнэ байх болтугай Дараа нь вектор функцийн скаляр аргументийн деривативыг дуудна

№17 Муруйн хөдөлгөөн дэх цэгийн хурд ба хурдатгал

Хурд

Хурдыг материаллаг цэгийн хөдөлгөөний шинж чанар болгон нэвтрүүлсэн. Хурд гэдэг нь тухайн үеийн хөдөлгөөний хурд (хурдны векторын хэмжээ) ба түүний чиглэл (хурдны векторын чиглэл) хоёуланг нь тодорхойлдог вектор хэмжигдэхүүн юм. Материаллаг цэгийг ямар нэгэн муруй шугамын дагуу хөдөлгөж, t хугацааны агшинд r0 радиус вектортой тохирч байна (Зураг 1). Богино хугацаанд Δt цэг нь Δs явах ба нэгэн зэрэг энгийн (хязгааргүй) шилжилтийг Δr хүлээн авна.

Дундаж хурдны вектор цэгийн радиус векторын Δr өсөлтийг Δt хугацааны интервалд харьцуулсан харьцаа гэнэ.

Дундаж хурдны векторын чиглэл нь Δr-ийн чиглэлтэй давхцдаг. Δt-ийн хязгааргүй бууралтаар дундаж хурд нь агшин зуурын хурд v гэж нэрлэгддэг утга руу чиглэнэ.

Энэ нь агшин зуурын хурд v нь вектор хэмжигдэхүүн бөгөөд цаг хугацааны хувьд хөдөлж буй цэгийн радиус векторын эхний деривативтай тэнцүү байна гэсэн үг юм. Учир нь хязгаарт, секант шүргэгчтэй давхцаж, дараа нь v хурдны вектор нь хөдөлгөөний чиглэлд траекторийн шүргэгч рүү чиглэнэ (Зураг 2).

Зураг 2

Δt буурах тусам Δs улам бүр |Δr|-д ойртох тул агшин зуурын хурдны модуль

Энэ нь агшин зуурын хурдны үнэмлэхүй утга нь цаг хугацааны хувьд замын эхний деривативтай тэнцүү байна гэсэн үг юм.

Тэгш бус хөдөлгөөнтэй үед агшин зуурын хурдны модуль нь өөр өөр цаг үед өөр өөр байдаг. Энэ тохиолдолд скаляр хэмжигдэхүүнийг ашиглана - жигд бус хөдөлгөөний дундаж хурд:

Хэрэв бид ds=vdt илэрхийллийг t-ээс t+Δt хүртэлх хугацаанд нэгтгэвэл (томъёо (2)-ыг үзнэ үү) Δt хугацаанд тухайн цэгийн туулсан замын уртыг олно.

Нэг жигд хөдөлгөөний үед агшин зуурын хурдны тоон утга тогтмол байна; Дараа нь илэрхийлэл (3) хэлбэрийг авна

t1-ээс t2 хүртэлх хугацааны туршид цэгийн туулсан замын уртыг интегралаар тодорхойлно.

ХУРДАГЧ

Тэгш бус жолоодох үед хурд нь цаг хугацааны явцад хэр хурдан өөрчлөгдөж байгааг мэдэх шаардлагатай байдаг. Хэмжээ ба чиглэлийн хурд өөрчлөгдөх хурдыг тодорхойлдог физик хэмжигдэхүүнийг хурдатгал гэж нэрлэдэг. Хавтгай хөдөлгөөн - авч үзэж буй системийн цэг бүрийн траекторууд нэг хавтгайд байрлах хөдөлгөөнийг авч үзье. V векторыг t цаг дээрх А цэгийн хурд гэж үзье. Δt хугацааны туршид цэг В байрлал руу шилжиж, хэмжээ болон чиглэлийн хувьд v-ээс ялгаатай, v1 + Δv-тэй тэнцүү хурдыг хүлээн авсан. v1 векторыг А цэг рүү шилжүүлж Δv-г олъё (Зураг 1).

t-ээс t+Δt хүртэлх интервал дахь жигд бус хөдөлгөөний дундаж хурдатгал нь Δv хурдны өөрчлөлтийг Δt хугацааны интервалд харьцуулсан харьцаатай тэнцүү вектор хэмжигдэхүүн юм.

Материалын цэгийн t цаг хугацааны агшин зуурын хурдатгал нь вектор хэмжигдэхүүн болно.

цаг хугацааны хувьд хурдны анхны деривативтай тэнцүү.

Δv векторыг хоёр бүрэлдэхүүн хэсэг болгон задалъя. Үүнийг хийхийн тулд А цэгээс (Зураг 1) v хурдны чиглэлд модуль нь v1-тэй тэнцүү AD векторыг зурна. Мэдээжийн хэрэг, Δvτ-тэй тэнцүү CD вектор нь Δt модуль хугацааны туршид хурдны өөрчлөлтийг тодорхойлдог: Δvτ=v1-v. Δv векторын Δvn хоёр дахь бүрэлдэхүүн хэсэг нь Δt чиглэлийн хурдны өөрчлөлтийг тодорхойлдог.

Хурдатгалын тангенциал бүрэлдэхүүн хэсэг:

өөрөөр хэлбэл, энэ нь хурдны модулийн цаг хугацааны анхны деривативтай тэнцүү бөгөөд ингэснээр модулийн хурдны өөрчлөлтийн хурдыг тодорхойлно.

Бид хурдатгалын хоёр дахь бүрэлдэхүүн хэсгийг хайж байна. Бид В цэгийг А цэгтэй маш ойрхон гэж таамаглаж байгаа тул Δs-ийг AB хөвчөөс арай өөр r радиустай тойргийн нум гэж үзэж болно. AOB гурвалжин нь EAD гурвалжинтай төстэй бөгөөд үүнээс Δvn/AB=v1/r-ийг дагадаг боловч AB=vΔt тул

Δt→0 дахь хязгаарт бид v1→v-г авна.

Учир нь v1→v, EAD өнцөг тэг болох хандлагатай ба түүнээс хойш EAD гурвалжин нь тэгш өнцөгт, тэгвэл v ба Δvn хоорондох ADE өнцөг нь тэгш өнцөгт чиглэнэ. Үүний үр дүнд Δt→0 үед Δvn ба v векторууд харилцан перпендикуляр болно. Учир нь хурдны векторыг траектор руу тангенциал чиглүүлж, дараа нь хурдны вектортой перпендикуляр Δvn вектор нь цэгийн траекторийн муруйлтын төв рүү чиглэнэ. Хурдатгалын хоёр дахь бүрэлдэхүүн хэсэг, тэнцүү

хурдатгалын хэвийн бүрэлдэхүүн хэсэг гэж нэрлэгддэг ба түүний муруйлтын төв рүү траекторийн шүргэгч (хэвийн гэж нэрлэдэг) перпендикуляр шулуун шугамын дагуу чиглүүлдэг (тиймээс үүнийг төв рүү чиглэсэн хурдатгал гэж нэрлэдэг).

Биеийн нийт хурдатгал нь тангенциал ба хэвийн бүрэлдэхүүн хэсгүүдийн геометрийн нийлбэр юм (Зураг 2):

Энэ нь хурдатгалын тангенциал бүрэлдэхүүн хэсэг нь үнэмлэхүй утга дахь хурдны өөрчлөлтийн хурдны шинж чанар (траектор руу тангенциал чиглэсэн), хурдатгалын хэвийн бүрэлдэхүүн хэсэг нь хурдны чиглэлийн өөрчлөлтийн хурдны шинж чанар юм. траекторийн муруйлтын төв). Хурдатгалын тангенциал болон хэвийн бүрэлдэхүүн хэсгүүдээс хамааран хөдөлгөөнийг дараах байдлаар ангилж болно.

1)aτ=0, an=0 - шулуун шугаман жигд хөдөлгөөн;

2)aτ=an=const, аn=0 - шулуун шугаман жигд хөдөлгөөн. Энэ төрлийн хөдөлгөөнөөр

Хэрэв эхний цаг t1 = 0, анхны хурд v1 = v0 бол t2=t ба v2 = v гэж тэмдэглэвэл бид a=(v-v0)/t-г олж авна.

Энэ томъёог тэгээс t хугацааны дурын момент хүртэлх мужид нэгтгэснээр жигд хувьсах хөдөлгөөний үед цэгийн туулсан замын уртыг олж мэднэ.

3)aτ=f(t), an=0 - хувьсах хурдатгалтай шулуун шугаман хөдөлгөөн;

4)aτ=0, an=const. aτ=0 үед хурд нь үнэмлэхүй утгаараа өөрчлөгддөггүй, харин чиглэл нь өөрчлөгддөг. an=v2/r томьёоноос харахад муруйлтын радиус тогтмол байх ёстой. Иймд дугуй хөдөлгөөн жигд байна, жигд муруй хөдөлгөөн;

5)aτ=0, an≠0 жигд муруйн хөдөлгөөн;

6)aτ=const, an≠0 - муруй шугаман жигд хөдөлгөөн;

7)aτ=f(t), an≠0 - хувьсах хурдатгалтай муруйн хөдөлгөөн.

No18 Гадаргуугийн шүргэгч хавтгай ба нормаль тэгшитгэл

Тодорхойлолт. Хоёр хувьсагчийн z =f(x,y) функцийг D мужид өгье, M0(x0;y0) нь D мужын дотоод цэг, M(x0+Δx;y+Δy) нь D "хөрш" M0.

Функцийн бүрэн өсөлтийг авч үзье:

Хэрэв Δz нь дараах байдлаар илэрхийлэгдэнэ.

Энд A, B нь тогтмолууд (Δx, Δy-ээс хамааралгүй), - M ба M0 хоорондын зай, α(Δ x,Δy) - Δx 0, Δy 0 үед хязгааргүй бага; тэгвэл z =f(x,y) функцийг М0 цэгт дифференциалагдах ба илэрхийлэл гэнэ

М0 цэг дээрх z =f(x;y) функцийн нийт дифференциал гэнэ.

Теорем 1.1. Хэрэв z =f(x;y) нь M0 цэгт дифференциал болох юм бол

Баталгаа

(1.16)-д Δx, Δy нь дурын хязгааргүй тоонууд тул Δy =0, Δx≠0, Δx 0, тэгвэл бид авч болно.

үүний дараа (1.16)-аас эхлэн дагана

Үүний нэгэн адил энэ нь батлагдсан

ба теорем 1.1. батлагдсан.

Тайлбар: M0 цэг дээрх z =f(x,y)-ийн дифференциал байдал нь хэсэгчилсэн дериватив байгааг илтгэнэ. Эсрэг заалт нь үнэн биш байна (M0 цэгт хэсэгчилсэн дериватив байгаа нь M0 цэгт ялгах чадвартай гэсэн үг биш).

Үүний үр дүнд теорем 1.1-ийг харгалзан томъёо (1.18) дараах хэлбэртэй болно.

Үр дагавар. M0 цэг дээрх дифференциалагдах функц энэ цэг дээр тасралтгүй байна ((1.17)-аас Δx 0, Δy 0-ийн хувьд: Δz 0, z(M) z(M0)) гэж гарна.

Тайлбар: Гурав ба түүнээс дээш хувьсагчийн хувьд мөн адил. Илэрхийлэл (1.17) дараах хэлбэртэй байна.

Хэсэгчилсэн деривативуудын геометрийн утгыг (Зураг 1.3) ашиглан гадаргууд шүргэгч хавтгай π кассын дараах тэгшитгэлийг (1.24) гаргаж болно: z =f(x,y) цэг дээр C0(x0,y0,z0), z0=z(M):

(1.24) ба (1.21)-ийн харьцуулалтаас бид хоёр хувьсагчийн функцийн нийт дифференциалын геометрийн утгыг олж авна.

С цэг нь С0 цэгээс цэг хүртэл шүргэгч хавтгайн дагуу шилжих үед хэрэглээний z-ийн өсөлт

хаанаас (1.24).

Гадаргуугийн хэвийн Lн-ийн тэгшитгэл: С0 цэг дэх z = f(x,y) нь шүргэгч хавтгайд перпендикуляр С0-ийг дайран өнгөрөх шулуун шугамын тэгшитгэлээр олно.

No 19 Чиглэлийн дериватив. Градиент

Функцийг зарим домэйнд өгье ба хугацаа . Чиглэл нь косинустай цэгээс вектор зуръя . Вектор дээр, түүний эхлэлээс хол зайд, цэгийг авч үзье, өөрөөр хэлбэл. .

Бид функц гэж таамаглах болно ба түүний 1-р эрэмбийн хэсэгчилсэн деривативууд домэйнд тасралтгүй байна.

at харьцааны хязгаарыг функцийн дериватив гэнэ цэг дээр векторын чиглэлд ба тэмдэглэгдсэн, i.e. .

Функцийн деривативыг олох өгөгдсөн цэг дээр векторын чиглэлд томъёог ашиглана уу:

Хаана – векторын чиглэлийн косинусууд , эдгээрийг томъёогоор тооцоолно:
.

Тодорхой бүсийн цэг бүрт функцийг зааж өгье .

Координатын тэнхлэг дээрх проекцууд нь харгалзах цэг дээрх энэ функцийн хэсэгчилсэн деривативуудын утгууд болох векторыг функцийн градиент гэж нэрлэдэг. болон томилогдсон буюу (“nabla u” гэж уншина уу): .

Энэ тохиолдолд тухайн бүсэд градиентийн вектор талбар тодорхойлогддог гэж тэд хэлэв.

Функцийн градиентийг олох өгөгдсөн цэг дээр томъёог ашиглана уу: .

No22 Тодорхойгүй интегралын үндсэн шинж чанарууд

Тодорхой бус интеграл

Энд F нь f функцийн эсрэг дериватив (интервал дээр); C нь дурын тогтмол юм.

Үндсэн шинж чанарууд

1.

2.

3. Хэрэв Тэр

24)

25)

28)

Энэ аргыг интеграл нь гетероген функцүүдийн үржвэр эсвэл коэффициент байх тохиолдолд ашигладаг. Энэ тохиолдолд V’(x)-ийг амархан нэгтгэдэг хэсэг гэж авна.

29)

32) Рационал бутархайг энгийн бутархай болгон задлах.

Аливаа зөв рационал бутархай
Эхний - дөрөв дэх төрлийн хязгаарлагдмал тооны энгийн рационал бутархайнуудын нийлбэрээр илэрхийлж болно. Задаргааны хувьд
хуваагчийг энгийн бутархай болгон өргөжүүлэх шаардлагатай Qm(x)тэгшитгэлийг шийдэх шаардлагатай шугаман ба квадрат хүчин зүйлүүд:

- (5)

Теорем.Зөв рационал бутархай
, Хаана
, Энгийн бутархайн нийлбэр болгон өвөрмөц байдлаар задалж болно:

- (6)

(A 1 , A 2 , …, A k , B 1 , B 2 , …, B 1 , M 1 , N 1 , M 2 , M 2 , …, M s , N s – зарим бодит тоо).

33) Зөв бутархайг хуваагчийн нийлмэл үндэс бүхий энгийн бутархай болгон задлах

Асуудлын томъёолол. Тодорхойгүй интегралыг ол

1 . Дараах тэмдэглэгээг танилцуулъя.

Тоолуур ба хуваагчийн зэргийг харьцуулж үзье.

Хэрэв интеграл нь буруу рационал бутархай бол, i.e. тоологч зэрэгn хувагчийн хүчнээс их буюу тэнцүү байнам , дараа нь эхлээд тоологчийг хуваагчаар хуваах замаар рационал функцийн бүх хэсгийг сонгоно.

Энд олон гишүүнт нь зэрэг болон хуваагдсаны үлдэгдэл юмPk(x) бага зэрэгQm

2 . Зөв рационал бутархайг өргөжүүлье

энгийн бутархай руу.

Хэрэв түүний хуваагч нь энгийн нийлмэл үндэстэй бол i.e.

дараа нь өргөтгөл нь хэлбэртэй байна

3 . Тодорхой бус коэффициентийг тооцоолохын тулдA1,A2,A3...B1,B1,B3... бид таних тэмдгийн баруун талд байгаа бутархайг нийтлэг хуваагч руу аваачиж, дараа нь коэффициентүүдийг ижил түвшинд тэнцүүлнэ.X зүүн ба баруун талд байгаа тоологчдод. Системээ авч үзье 2 С бүхий тэгшитгэлүүд 2 С үл мэдэгдэх, өвөрмөц шийдэлтэй.

4 Бид маягтын энгийн бутархайг нэгтгэдэг

47) Хэрэв интеграл нийлбэрийн төгсгөлөг I хязгаар λ → 0 байх ба энэ нь ξ i цэгийг сонгох арга, хэрчмийг хуваах аргаас хамаарахгүй бол энэ хязгаарыг f функцийн тодорхой интеграл гэнэ. x) сегментийн дээгүүр байх ба дараах байдлаар тэмдэглэнэ.

Энэ тохиолдолд f (x) функцийг дээр интегралчлах боломжтой гэнэ. a ба b тоонуудыг интегралын доод ба дээд хязгаар гэж нэрлэдэг бөгөөд f (x) нь интеграл, x нь интегралын хувьсагч юм. Тодорхой интегралын интеграцийн хувьсагчийг аль үсэг илэрхийлэх нь хамаагүй гэдгийг тэмдэглэх нь зүйтэй.

Учир нь ийм төрлийн тэмдэглэгээг өөрчлөх нь интеграл нийлбэрийн төлөв байдалд ямар ч байдлаар нөлөөлөхгүй. Тэмдэглэгээ, нэр томьёоны хувьд ижил төстэй хэдий ч тодорхой ба тодорхойгүй интеграл нь ялгаатай

48) Тодорхой интеграл байх тухай теорем

Хэсэгийг х1,х2,х3 цэгээр хэсэг болгон хуваая... тэгэхээр

i-р хэсгийн уртыг deltaX-ээр ба эдгээр уртын хамгийн их хэмжээгээр тэмдэглэе.

Хэсэг тус бүрийн тодорхой цэгийг дур мэдэн сонгоод (үүнийг "дунд цэг" гэж нэрлэдэг) дарааллаар бичье.

интеграл нийлбэр гэж нэрлэгддэг хэмжигдэхүүн

Одоо хязгаараа олцгооё

Тодорхойлолт. Хэрэв энэ нь байгаа бөгөөд энэ нь хамаарахгүй бол

a) сегментийг хэсэг болгон хуваах арга ба -аас

б) дунд цэгийг сонгох арга,

сегмент дээрх f(x) функцийн тодорхой интеграл юм.

Энэ тохиолдолд f(x) функцийг интервал дээр интегралдах боломжтой гэж нэрлэдэг. a ба b хэмжигдэхүүнийг интегралын доод ба дээд хязгаар гэж нэрлэдэг.

50) Тодорхой интегралын үндсэн шинж чанарууд

1) Хэрэв интегралын интервал нь хязгаарлагдмал тооны хэсэгчилсэн интервалд хуваагдвал интервал дээр авсан тодорхой интеграл нь түүний бүх хэсэгчилсэн интервалд авсан тодорхой интегралын нийлбэртэй тэнцүү байна.

2) дундаж утгын теорем.

y = f(x) функцийг ,m=min f(x) ба M=max f(x) интервал дээр интегралчлах боломжтой байг, тэгвэл ийм тоо байна.

Үр дагавар.

y = f(x) функц нь интервал дээр тасралтгүй байвал ийм тоо байна.

3) Интегралын хязгаарыг дахин зохион байгуулахдаа тодорхой интеграл тэмдэгээ эсрэгээр өөрчилдөг.

4) Интегралын ижил хязгаартай тодорхой интеграл тэгтэй тэнцүү байна.

5) Функцийн модулийг нэгтгэх

Хэрэв f(x) функц интегралдах боломжтой бол түүний модуль нь мөн интервал дээр интегралдах боломжтой.

6) Тэгш бус байдлын интеграл

Хэрэв f(x) ба q(x) нь интервал дээр интеграл болох ба x-д хамаарах бол

Тэр

7) Шугаман байдал

Тогтмол хүчин зүйлийг тодорхой интегралын тэмдгээс цааш авч болно

хэрэв f(x) байгаа ба интервал дээр интегралдах боломжтой бол A=const

Хэрэв y=f(x) функц нь интервал дээр тасралтгүй бөгөөд F(x) нь (F’(x)=f(x)) дээр түүний эсрэг деривативуудын аль нэг нь байвал томъёо нь биелнэ.

Тасралтгүй функцийн интегралыг тооцохдоо x=α(t) орлуулалтыг хийцгээе.

1) x=α(t) функц ба түүний дериватив x’=α’(t) нь t-д хамаарах тасралтгүй байна.

2) t дахь x=α(t) функцийн утгуудын багц нь сегментэд хамаарна

3) A α(c)=a ба α(v)=b

f(x) функц интервал дээр тасралтгүй байх ба x=b үед хязгааргүй тасралттай байг. Хэрэв хязгаар байгаа бол түүнийг хоёр дахь төрлийн зохисгүй интеграл гэж нэрлэдэг ба -аар тэмдэглэнэ.

Тиймээс, тодорхойлолтоор,

Хэрэв баруун гар талын хязгаар байгаа бол буруу интеграл байна нийлдэг.Хэрэв заасан хязгаар байхгүй эсвэл хязгааргүй бол интеграл гэж хэлдэг ялгаатай.

ба түүний ялгаа.

Орон зайн муруйг тодорхойлох хамгийн энгийн аргуудын нэг бол вектор тэгшитгэлийг тодорхойлох явдал юм.

Хаана нь муруйн цэгийн радиус вектор, ба - цэгийн байрлалыг тодорхойлох параметр.

Тэр. хувьсах вектор скаляр функц байдаг . Математикийн шинжилгээнд ийм функцийг скаляр аргументийн вектор функц гэж нэрлэдэг.

Задардаг Нэгж векторуудыг ашиглан тэгшитгэл (1)-ийг дараах хэлбэрээр өгч болно.

Энэхүү өргөтгөл нь муруйны параметрийн тэгшитгэл рүү шилжих боломжийг олгодог.

Өөрөөр хэлбэл, вектор функцийг зааж өгөх нь гурван скалярыг зааж өгсөнтэй тэнцэнэ.

Энэ муруйг тодорхойлсон вектор функц (1)-тэй холбоотойгоор муруйг өөрөө энэ функцийн годограф гэж нэрлэдэг. Энэ тохиолдолд координатын гарал үүслийг годографын туйл гэж нэрлэдэг.

Одоо больё
Тэгээд
- (1) тэгшитгэлээр тодорхойлсон муруйн цэгүүд. Түүнээс гадна
, А
Эдгээр цэгүүдийн радиус векторууд нь байх болно

Тэгээд
.

Вектор
вектор функцийн өсөлт гэж нэрлэдэг
, өсөлттэй харгалзах
түүний аргумент бөгөөд үүнийг тэмдэглэнэ
,

Вектор функц
тасралтгүй функц байх болно , Хэрэв

.

-ийн деривативыг олох
дараах байдлаар үргэлжлүүлье -

.

Одоо чиглэлээ тогтооцгооё
. Энэ нь ойлгомжтой -тай таарч байна
болон цагт
-тэй ижил чиглэлд чиглэсэн
Тэгээд хэзээ
- эсрэг чиглэлд. Гэхдээ эхний тохиолдолд
болон хоёрдугаарт
Тэр. вектор үргэлж секант годографын дагуу чиглүүлдэг
дээшээ .

Хэрэв бид өргөтгөлийг ашиглавал Тэгээд дараа нь orts

Эндээс (*) -ийг хуваана
мөн хязгаар руугаа явж байна
Учир нь
бид авдаг

(4)-д үндэслэн дараах томъёонууд хүчинтэй болохыг харуулж болно.

(5)

(6)

- скаляр функц.

Нотлох баримт (7).

Одоо зарим шинж чанарыг авч үзье
. Юуны өмнө түүний модулийг олъё:

.

Учир нь Бид годографын нумыг засч залруулах боломжтой гэж үздэг
- хөвчний урт, ба
- нумын урт. Тийм ч учраас

Тэр. скаляр аргументийн вектор функцийн деривативын модуль нь ижил аргументтай харьцуулахад годограф нумын деривативтай тэнцүү байна.

Дүгнэлт 1. Хэрэв - өсөх чиглэлд годограф руу тангенциал чиглэсэн нэгж вектор , Тэр

Дүгнэлт 2. Годографын нумын уртыг вектор функцийн аргумент болгон авбал , Тэр

(учир нь
)

Тэр. годографын нумын уртын дагуух вектор функцийн дериватив нь нумын уртыг нэмэгдүүлэхэд чиглэсэн ходограф руу шүргэгчийн нэгж вектортой тэнцүү байна.

Дүгнэлт 3. Хэрэв вектор функцийн годографыг цэгийн траектор гэж үзвэл ба - хөдөлгөөний цагийг тодорхой үеэс тоолно , Тэр
хөдөлгөөний хурдны вектортой хэмжээ болон чиглэлийн хувьд давхцдаг
.

Үнэн хэрэгтээ хурдны скаляр утга нь цаг хугацааны хувьд замын деривативтай тэнцүү байна.

Үүнээс гадна вектор өсөлтийн чиглэлтэй тохирч байгаа хөдөлгөөний чиглэлд траектор руу тангенциал чиглүүлсэн , өөрөөр хэлбэл чиглэлтэй тохирч байна .

Тэр.
.

Одоо авч үзье
урт нь тогтмол,
, өөрөөр хэлбэл

(*)
Хаана

(*) ялгахдаа бид дараахыг олно.

Тэдгээр.

Ялангуяа нэгжийн чиглэлд дурын хувьсагчийн векторын дериватив Үргэлж
.

Одоо больё
цэгүүдэд зурсан нэгж бөмбөрцгийн радиусуудын хоорондох өнцөг
Тэгээд
годограф
. Дараа нь хөвчний урт
гурвалжингаас
тэнцүү байх болно

Нэгж хувьсах векторын деривативын хэмжээ нь энэ векторын эргэлтийн өнцгийн хурдтай тэнцүү байна.

Скаляр функцүүдийн хувьд вектор функцийн дифференциалыг дараах байдлаар бичнэ

Гэхдээ тэр үед ч гэсэн

Орон зайн муруйн муруйлт.

Дагалдах гурвалжин.

Дүгнэлт 2-ын дагуу, төлөө Бид томъёог бичиж болно:

Чиглэлээ өөрчлөх , орон зайн муруй руу шүргэгчийн өөрчлөлттэй холбоотой, муруйн муруйлтыг тодорхойлдог. Орон зайн муруйн муруйлтыг хэмжихдээ хавтгай муруйны хувьд зэргэлдээх өнцгийг нумын урттай харьцуулах хязгаарыг авна.

муруйлт,
зэргэлдээх өнцөг,
нумын урт.

Нөгөө талаар,
нэгж вектор ба түүний дериватив вектор перпендикуляр ба түүний модуль
Ялгах By болон орох
чиглэлтэй нэгж вектор , бид олдог:

Вектор
орон зайн муруйн муруйлтын вектор. Шүргэх чиглэлтэй перпендикуляр чиглэл нь сансрын муруйны хэвийн чиглэл юм. Гэхдээ орон зайн муруй нь аль ч цэгт хязгааргүй тооны нормальтай байдаг бөгөөд тэдгээр нь бүгд муруйны өгөгдсөн цэгийг дайран өнгөрч, өгөгдсөн цэг дэх шүргэгчтэй перпендикуляр байдаг хавтгайд оршдог. Энэ хавтгайг орон зайн муруйн хэвийн хавтгай гэж нэрлэдэг.

Тодорхойлолт. Муруйн муруйлт вектор өгөгдсөн цэгт чиглэсэн муруйн хэвийн хэмжээ нь орон зайн муруйн үндсэн нормаль юм. Тэр.
нэгж үндсэн хэвийн вектор.

Одоо гурав дахь нэгж векторыг байгуулъя хөндлөн бүтээгдэхүүнтэй тэнцүү байна Тэгээд

Вектор , түүнчлэн мөн перпендикуляр тэдгээр. ердийн хавтгайд байрладаг. Түүний чиглэлийг өгөгдсөн цэг дэх орон зайн муруйн бинормалын чиглэл гэж нэрлэдэг. Вектор
Тэгээд нь харилцан перпендикуляр нэгж векторуудын гурвалыг бүрдүүлдэг бөгөөд тэдгээрийн чиглэл нь орон зайн муруй дээрх цэгийн байрлалаас хамаардаг ба цэгээс цэг хүртэл харилцан адилгүй байдаг. Эдгээр векторууд гэж нэрлэгддэг зүйлийг бүрдүүлдэг. орон зайн муруйн дагалддаг триэдрон (Frenet trihedron). Вектор
Тэгээд Нэгж нэгж векторуудын нэгэн адил зөв гурвалсан хэлбэрийг үүсгэнэ
зөв координатын системд.

Хосоор авсан
муруйн ижил цэгийг дайран өнгөрч, дагалдах гурван өнцөгтийн нүүрийг бүрдүүлдэг гурван хавтгайг тодорхойлно. Хаана Тэгээд osculating хавтгайг тодорхойлох (өгөгдсөн цэгийн ойролцоох муруй нум нь илүү өндөр эрэмбийн нарийвчлалтайгаар хэлбэлзэх хавтгай дахь хавтгай муруй нум юм);

Тэгээд - тэгшлэх хавтгай;

Тэгээд - ердийн онгоц.

Тангенс, хэвийн ба хоёр хэвийн тэгшитгэл.

Дагалдах гурван өнцөгтийн хавтгайн тэгшитгэл.

Мэдэх
Тэгээд , эсвэл тэдгээрт коллинеар нэгж бус векторууд Т, НТэгээд БЭнэ хэсэгт нэрлэгдсэн тэгшитгэлүүдийг гаргаж авцгаая.

Үүнийг хийхийн тулд шулуун шугамын каноник тэгшитгэлд

өгөгдсөн цэгийг дайран өнгөрөх хавтгайн тэгшитгэлд

авах
муруй дээр сонгосон цэгийн координат, хувьд
эсвэл тус тусад нь
векторуудын координатыг авна
эсвэл
, энэ нь хүссэн шугамын чиглэл эсвэл хүссэн хавтгайд хэвийн чиглэлийг тодорхойлдог:

эсвэл - шүргэгч эсвэл ердийн хавтгайд;

эсвэл - үндсэн хэвийн ба тэгшлэх хавтгайд,

эсвэл - бинормаль ба оскулятор хавтгайд зориулагдсан.

Хэрэв муруйг вектор тэгшитгэлээр өгвөл
эсвэл
дараа нь векторын хувьд
тангенциалаар чиглэсэн авч болно

Олох
Тэгээд эхлээд задралыг олъё
вектороор
Өмнө нь (Үндэслэл 1) бид үүнийг олж мэдсэн
-ээр ялгах , бид авах:

Гэхдээ, учир нь

Одоо вектороор үржүүлье Тэгээд

(*)

Вектор бүрт (*) үндэслэсэн , хоёр хэвийн чиглэлтэй бол бид векторыг авч болно

Харин дараа нь
Бид эдгээр сүүлчийн вектор үржвэрийг авч болно:

Тэр. дурын муруйн аль ч цэг дээр бид дагалдаж байгаа гурвалжингийн бүх элементүүдийг тодорхойлж чадна.

Жишээ. Дурын цэгт баруун мушгиа руу шүргэгч, хэвийн ба хоёрнормалын тэгшитгэл.

Тангенс

Гэрийн хэвийн

Хоёр хэвийн

Depositfiles-аас татаж авах

ДИФФЕРЕНЦИАЛ ГЕОМЕТР

I. СКАЛАР АРГУМЕНТИЙН ВЕКТОР функц

Вектор функц (тодорхойлолт 1.1), түүнийг тодорхойлох аргууд.

Радиус вектор ба ходограф, параметрт ходографын тодорхойлолт.

Вектор функцийн дериватив (Тодорхойлолт 1.6).

Вектор функцийн деривативын геометрийн утга.

Вектор функцийг ялгах дүрэм.

1.1. ВЕКТОР ФУНКЦИЙН ТОДОРХОЙЛОЛТ

Тодорхойлолт 1.1Хэрэв скаляр аргументийн утга тус бүртохирсон вектор
гурван хэмжээст орон зай R 3 , дараа нь тэд скаляр аргументын вектор функц (эсвэл вектор функц) X олонлог дээр өгөгдсөн гэж хэлдэг.т .

Хэрэв сансарт байгаа бол R 3 Декартын координатын системийг тодорхойлсонТУХАЙ xyz , тэгвэл даалгавар нь вектор - функц болно
,
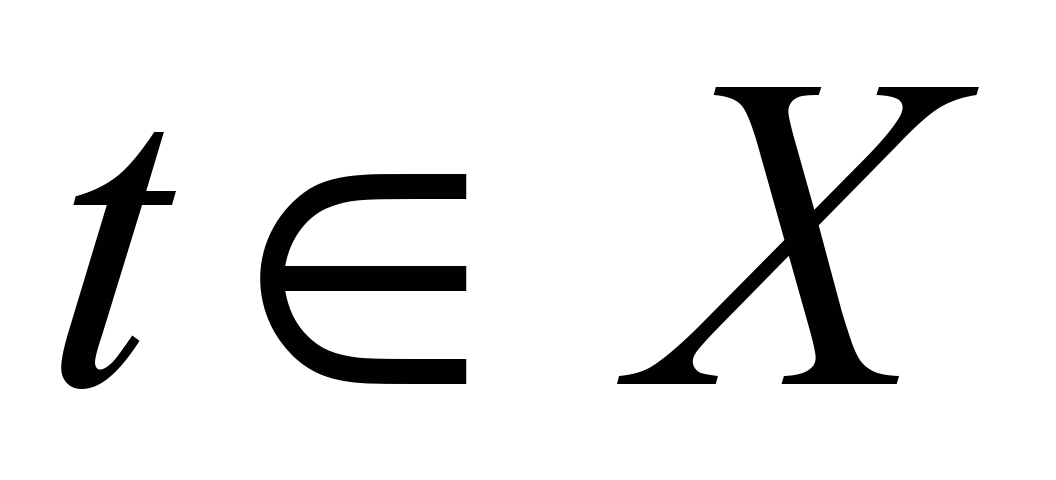гурван скаляр функцийг зааж өгсөнтэй тэнцэнэX( т ), y ( т ), z ( т ) - вектор координатууд:

= { x ( т ), y ( т ), z ( т )} (1.1)

эсвэл , (1.2)

Хаана
— координатын нэгж векторууд.

1.2. РАДИУС ВЕКТОРЫН ХОДОГРАФ ГАРСАН ОРОН САЙН ШУГАМ

Тодорхойлолт 1.2 Хэрэв бүх векторын эхлэл нь ,гарал үүсэл дээр байрлуулсан бол тэдгээрийг радиус вектор гэж нэрлэдэг.

Тодорхойлолт 1.3 , , радиус векторуудын төгсгөлүүдийн геометрийн байрлал болох шугамыг вектор функцийн годограф гэж нэрлэдэг ба тэдгээрийн нийтлэг эхлэл нь годографын туйл юм.

Хэрэв параметр т цаг хугацаа ба хөдөлж буй цэгийн радиус вектор бол функцийн годограф нь хөдөлж буй цэгийн траектор юм.

Годографын тэгшитгэлийг вектор хэлбэрээр (1.2) эсвэл параметрийн хэлбэрээр бичиж болно.

(1.3)

Ялангуяа вектор функц боларгументыг өөрчилснөөр зөвхөн түүний модуль өөрчлөгддөг боловч чиглэл өөрчлөгддөггүй (), тэгвэл ийм вектор функцийн годограф нь эх үүсвэрээс гарч буй шулуун шугаман туяа байх болно; Хэрэв зөвхөн векторын чиглэл өөрчлөгдөх боловч түүний хэмжээ өөрчлөгдөөгүй хэвээр байвал (
), тэгвэл векторын функцийн годограф нь төв нь туйлд байх ба векторын тогтмол модультай тэнцүү радиустай бөмбөрцөг дээр байрлах муруй байх болно.

Зураг 1.

1.3. ВЕКТОР-ФУНКЦИЙН ХЯЗГААР, ҮРГЭЛЖЛЭЛ, ҮҮСЭЛ

Тодорхойлолт 1. 4 Вектор вектор функцийн хязгаар гэж нэрлэдэгцагт
, Хэрэв

. (1.4)

Тодорхойлолт 1.5Вектор функц гэж нэрлэдэг нэг цэг дээр тасралтгүйт 0, Хэрэв энэ цэг дээрх вектор функцийн утгатай тэнцүү хязгаартай бол:

. (1.5)

Тодорхойлолт 1.6Вектор функцийн деривативцэг дээр т вектор функцийн өсөлтийг аргументийн өсөлттэй харьцуулсан харьцааны хязгаар гэнэ
цагт
:

(1.6)

1.4. ВЕКТОР ФУНКЦИЙН АНХНЫ ҮҮСГЭЛИЙН ГЕОМЕТРИЙН БОЛОН МЕХАНИК УТГА

Скаляр аргументийн вектор функцын анхны деривативын геометрийн утга нь энэ дериватив нь годограф руу тангенциал чиглэсэн шинэ вектор юм.
. Үүнийг үзүүлье.

Зураг 2

Бид авч үзэж буй вектор функцийн годограф нь ямар ч цэгт шүргэгчтэй тасралтгүй шулуун байна гэж таамаглах болно.

Аргументаа өгье т өсөлт, дараа нь геометрийн харьцаа
зарим вектор юм
, секант ММ' дээр хэвтэж байна. Энэ вектор эргэлдэж, вектор болж хувирах үед
, шүргэгч дээр хэвтэж, өсөлт рүү чиглэсэнт . Тэгэхээр вектор

(1.7)

параметрийн өсөлтийн чиглэлд чиглэсэн нэгж тангенс вектор байх болнот .

Тиймээс вектор
цэг дээрх муруйн шүргэгч чиглэлийн векторыг ), (эсвэл
), шүргэгч тэгшитгэлийг дараах хэлбэрээр бичнэ.

(1.8)

Хэрэв т – цаг хугацаа, ба - цэгийн радиус вектор
, гурван хэмжээст орон зайд хөдөлж, дараа нь ойролцоогоорхамаарлыг сегмент дэх цэгийн дундаж хурд гэж нэрлэдэг [т; т+т].

Механик утгавектор функцийн анхны дериватив нь энэ дериватив нь тухайн үеийн М цэгийн хурдыг илэрхийлдэгт :

Вектор функцийг ялгах дүрэм

Векторыг хасах, векторыг тоонд хуваах дүрмийг ашиглан 1-р дүрмийг баталъя:

Үлдсэн дүрмийн баталгаа нь 1-р дүрэм болон векторуудтай ажиллах дүрэмд үндэслэсэн болно.

Жишээ 1.1: Вектор функц өгөгдсөн.Түүний годографыг байгуулж, дурын цэг дээрх шүргэгчийн тэгшитгэлийг үүсгэ.

Шийдэл. Ямар ч цэгийн хувьд ( x , y , z ) годограф вектор – бидэнд байгаа функцууд:x = acost ; y = asint ; z = bt мөн тиймээс аливаад
тэгш байдал хадгалагданаx 2 + y 2 = а 2 , ба generatrix нь тэнхлэгтэй зэрэгцээ байнаОз. Хэрэв параметр т цаг хугацаа гэж тайлбарлаж, дараа нь тойрог тойрон жигд хөдөлгөөнөөр радиус векторын төгсгөлийн проекцийг хавтгайд хийнэ.Окси тэнхлэг дээрх түүний проекцОз хурдтай жигд ба шулуун шугамаар хөдөлнөб . Өөрөөр хэлбэл, вектор функцийн годограф цэгийн хэрэглүүр нь түүний хавтгай дээрх проекцын эргэлтийн өнцөгтэй пропорциональ өсдөг.Окси . Иймд хүссэн годограф нь 3-р зурагт үзүүлсэн хэлбэртэй байх бөгөөд үүнийг мушгиа шугам гэж нэрлэдэг. Годографын шүргэгчийг олохын тулд вектор функцийн деривативыг олно.

Шийдэл. Учир нь, дараа нь

Тодорхойлолт 1. Зөвшөөрөгдөх утгуудын муж дахь скалярын утга бүр r векторын тодорхой утгатай тохирч байвал g векторыг t скаляр аргументын вектор функц гэнэ.Бид үүнийг дараах байдлаар бичнэ: Хэрэв вектор r нь скаляр аргументын функц t бол g векторын x, y, z координатууд нь мөн t аргументын функцууд байх болно: Скаляр аргументын вектор функц. Годограф. Скаляр аргументийн вектор функцийн хязгаар ба тасралтгүй байдал.Харин эсрэгээр, g векторын координатууд нь t%-ийн функц байвал g вектор өөрөө t-ийн функц болно: Иймд r(f) вектор функцийг тодорхойлох нь дараах байдалтай байна. y(t), z( t) гэсэн гурван скаляр функцийг зааж өгсөнтэй тэнцэнэ. Тодорхойлолт 2. Скаляр аргументын r(t) вектор функцийн годограф нь скаляр t өөрчлөгдөх үед r(*) векторын төгсгөл, r(f) векторын эхлэл байх үед цэгүүдийн байрлал юм. орон зайд тогтмол О цэг дээр байрлуулсан (Зураг I ). Сахалны векторын r = g(*) хөдөлгөөнд зориулсан годограф Зураг. 1 шатаах цэг нь энэ цэгийн траектори L байх болно. Энэ цэгийн хурдны годограф v = v(J) нь өөр L\ шугам байх болно (Зураг 2). Тэгэхээр, хэрэв материаллаг цэг тогтмол хурдтай тойрог хэлбэрээр хөдөлдөг бол |v| = const, тэгвэл түүний хурдны годограф нь мөн 0\ цэгт төвтэй, |v|-тэй тэнцүү радиустай тойрог байна. Жишээ 1. r = ti + t\ + t\ векторын годографыг байгуул. Шийдэл. 1. Энэ бүтээн байгуулалтыг цэгээр хийж, хүснэгт хийж болно: Зураг 3 2i Та мөн адил хийж болно. V векторын координатыг x, y, z-ээр тэмдэглэвэл Hts ба эдгээр тэгшитгэлийн гол түлхүүр нь 1Y параметр нь y - z = x1 гадаргуугийн тэгшитгэлийг олж авах бөгөөд L огтлолцлын шугам нь годографыг тодорхойлох болно. z() векторын (Зураг 3). D> Бие даасан шийдлийн даалгавар. Векторуудын годографуудыг байгуул: r = скаляр аргумент t вектор функцийг t аргументын утгын зарим хэсэгт 1-ийн өргөтгөлтэй ижил утгын хувьд тодорхойлъё. А тогтмол векторыг 1-ийн хязгаар гэнэ. вектор r(t) at, хэрэв аль нэг e > 0-ийн хувьд b > 0 байвал 11-р нөхцөлийг хангасан бүх t φ-ийн хувьд тэгш бус байдал биелнэ.Уламжлалт анализын нэгэн адил limr(0=A. Зураг 4 геометрийн хувьд, энэ нь вектор) гэж t -* to вектор руу чиглэнэ гэсэн үг Мөн урт болон чиглэлд хоёулаа (Зураг 4). Тодорхойлолт 2. a(£) векторыг t -» -д хязгааргүй жижиг гэнэ, хэрэв a(£) нь t -* to -д хязгаартай ба энэ хязгаар тэгтэй тэнцүү бол: Скаляр аргументийн вектор функц. Годограф. Скаляр аргументийн вектор функцын хязгаар ба тасралтгүй байдал эсвэл аль нэг e-ийн хувьд ижил байх 6 > 0 байгаа тул нөхцөлийг хангах бүх t Ф хувьд |a(£)| жишээ 1. Вектор нь t -* 0-д хязгааргүй час улаан вектор болохыг харуул. Шийдэл. Хэрэв ямар нэгэн e 0-ийн хувьд бид 6 = ~ гэж авбал -0|-д байгаа нь тодорхой байна бид тэмдэглэнэ |. Тодорхойлолтоор бол a(t) нь t 0 үед хязгааргүй вектор байна. r бие даасан шийдвэрлэх 1> бодлого.Сүүлийн хязгаар нь векторын модулийн хязгаар нь түүний хязгаарын модультай тэнцүү болохыг харуул. байдаг. . r(*) вектор функц нь А хязгаартай байхын тулд r(-г скаляр аргументийн Вектор функц хэлбэрээр илэрхийлж болно. Годограф. А-ийн вектор функцийн хязгаар ба тасралтгүй байдал шаардлагатай бөгөөд хангалттай гэдгийг батал. скаляр аргумент de a( t) - t -* t0-ийн хувьд векторыг эцэс төгсгөлгүй хөдөлгө.14. a+ b(*) вектор функц нь t = t0-д тасралтгүй байна.Үүнээс үзэхэд a(t) ба b( векторууд гарч байна уу? J) нь t - -ээс ?-ийн хувьд мөн тасралтгүй 15. Хэрэв a( тасралтгүй вектор функц бол тэдгээрийн скаляр үржвэр (a(*),b(f)) ба вектор үржвэр |a(f),b(t) болохыг батал. )] мөн тасралтгүй байна.

Жишээ 2.Жишээлбэл, гурван хувьсагчийн функцийг авч үзье е(X,цагт,z), дараах үнэний хүснэгттэй байна.

Хувьсах утгын векторуудын лексикографийн дарааллаар  X nтэдгээрийг орхигдуулж болох бөгөөд функц нь өөрөө бүрэн тодорхойлогдох болно үнэний утгын вектор е= (10110110).

Матрицын арга

Гол нь олон хувьсагч байдаг  X nхоёр хэсэгт хуваагдана  цагт мТэгээд  z n–mвекторын бүх боломжит үнэний утгууд байх болно  цагт мматрицын эгнээний дагуу зурсан бөгөөд векторын бүх боломжит үнэний утгууд  z n - м- баганаар. Функцийн үнэний утгууд ебагц бүр дээр   n = ( 1 , ...,  м ,  м+ 1 ,...,  n) шугамын огтлолцол үүссэн нүднүүдэд байрлуулна ( 1 , ...,  м) ба багана ( м+ 1 ,...,  n).

Дээр авч үзсэн 2-р жишээнд хувьсагчдыг хуваах тохиолдолд ( x, y, z) дэд олонлогт ( X) Тэгээд ( у, з) матриц нь дараах хэлбэртэй байна.

	у,z

Матрицын аргын чухал шинж чанар нь хувьсагчдын бүрэн багц юм  X n, хөрш зэргэлдээ (босоо болон хэвтээ) нүднүүдэд харгалзах нь нэг координатаар ялгаатай.

Бүтэн хоёртын модыг ашиглан зааж өгч байна

Тодорхойлолтын хувьд n- орон нутгийн функц е( X n) хоёртын модны өндрийн шинж чанарыг ашигладаг n, энэ нь унжлагааны орой бүр тодорхой вектор утгын багцтай нэг нэгээр нь тохирч байгаа явдал юм.  X n. Үүний дагуу энэ өлгөөтэй оройд функц нь энэ олонлогт байгаа үнэний утгыг оноож болно е. Жишээ болгон (Зураг 1.3) бид дээр дурдсан гурвалсан функцийн хоёртын модыг ашиглан даалгаврыг танилцуулж байна. f =(10110110).

Модны өлгөөтэй оройнуудад оноогдсон тоонуудын эхний эгнээ нь багцын лексикографийн дугаарыг, хоёр дахь нь багц өөрөө, гурав дахь нь түүн дээрх функцын утгыг илэрхийлдэг.

Ашигласан даалгаварn - хэмжээст нэгж шооIN n

Топуудаас хойш IN nмөн бүх багцын багцад нэг нэгээр нь буулгаж болно  X n, Тэр n- орон нутгийн функц е(X n) кубын харгалзах оройнуудад түүний үнэний утгыг оноож тодорхойлж болно IN n . Зураг 1.4-т функцийн тохиргоог харуулав е= (10110110) Кубад IN 3. Үнэний утгыг кубын оройд оноодог.

Тодорхойлолт . Логикийн алгебрБулийн тогтмол ба хувьсагчдын багцыг тэдгээрт оруулсан логик холболтын хамт нэрлэнэ үү.

Томъёоны даалгавар

Логик алгебрийн функцуудыг аналитик илэрхийлэл болгон тодорхойлж болно.

Тодорхойлолт. Болъё X― логик алгебрт хэрэглэгддэг хувьсагч ба тогтмолуудын цагаан толгой, Ф― 2-оос дээш тооны хувьсагчтай бүх энгийн функцүүдийн тэмдэглэгээ ба тэдгээрийн ерөнхий дүгнэлт.

X,F дээрх томьёо(логик алгебрийн томъёо) маягтын бүх бичлэгийг дуудъя:

A) X,Хаана X X;

б)  Ф 1 , Ф 1 &Ф 2 ,Ф 1 Ф 2 , Ф 1 Ф 2 , Ф 1  Ф 2 , Ф 1 Ф 2 ,Ф 1 Ф 2 ,Ф 1 Ф 2 , Хаана Ф 1 , Ф 2 - томъёо дууссан X, F;

V) h(Ф 1 , … ,Ф n ), Хаана n > 2, Ф 1 ,… ,Ф n- томьёо дууслаа X,Ф, h ― -аас ерөнхийжүүлсэн босго функцийн тэмдэглэгээ Ф .

Тодорхойлолтоос харахад хоёр оронтой энгийн функцүүдийн хувьд функциональ тэмдгийг аргументуудын хооронд байрлуулсан тэмдэглэгээний инфикс хэлбэрийг ашигладаг; үгүйсгэх болон ерөнхий функцүүдийн хувьд функциональ тэмдэг бүхий тэмдэглэгээний угтвар хэлбэрийг ашигладаг. аргументуудын жагсаалтын өмнө байрлана.

Жишээ 3.

1. Илэрхийлэл X(цагтz); ( x, y, z  у) нь дээр дурдсан тодорхойлолтыг хангаж байгаа тул логикийн алгебрийн томьёо юм.

2. Илэрхийлэл  X (цагт z)  үйлдлийг буруу хэрэглэсэн учир логик алгебрийн томьёо биш юм .

Тодорхойлолт. F томъёогоор хэрэгжсэн функц, нь хувьсагчдын утгыг орлуулах замаар олж авсан функц юм Ф.Үүнийг тэмдэглэе е(Ф).

Жишээ 4.Томьёог анхаарч үзээрэй Ф=xy (Xz). Хэрэгжүүлсэн функцийн үнэний хүснэгтийг байгуулахын тулд логик холболтын хүчийг харгалзан логик үржүүлгийг дэс дараалан гүйцэтгэх шаардлагатай. xy, дараа нь далд утга ( Xz), дараа нь үр дүнгийн үнэний утгыг модул 2 нэмнэ. Үйлдлүүдийн үр дүнг хүснэгтэд үзүүлэв.

				X z

Функцуудын томъёолол нь функцүүдийн олон шинж чанарыг априори үнэлэх боломжийг олгодог. Томъёоны даалгавараас үнэний хүснэгт рүү шилжих нь үнэний утгыг томъёонд багтсан энгийн функц болгон дараалан орлуулах замаар үргэлж хийж болно. Ижил функцийг өөр өөр томъёогоор илэрхийлж болох тул урвуу шилжилт нь хоёрдмол утгатай. Үүнийг тусад нь авч үзэх шаардлагатай.