राज्य बजटीय शैक्षणिक संस्थान

समारा क्षेत्र माध्यमिक सामान्य शिक्षा

स्कूल नंबर 2 के नाम पर रखा गया। वी. मस्किना रेलवे कला। Klyavlino

क्लाइवलिंस्की नगरपालिका जिला

समारा क्षेत्र

« समीकरण

और

असमानता

मापदंडों के साथ"

ट्यूटोरियल

Klyavlino

ट्यूटोरियल

"पैरामीटर के साथ समीकरण और असमानताएं"कक्षा 10-11 के छात्रों के लिए

यह मैनुअल वैकल्पिक पाठ्यक्रम "मापदंडों के साथ समीकरण और असमानताएं" के कार्यक्रम का एक परिशिष्ट है, जिसने एक बाहरी परीक्षा उत्तीर्ण की है (19 दिसंबर, 2008 को समारा क्षेत्र के शिक्षा और विज्ञान मंत्रालय की वैज्ञानिक और पद्धति विशेषज्ञ परिषद ने इसके लिए सिफारिश की थी) समारा क्षेत्र के शैक्षणिक संस्थानों में उपयोग)

लेखक

रोमाडानोवा इरीना व्लादिमीरोवाना

क्लाइवलिंस्काया माध्यमिक शैक्षणिक संस्थान में गणित के शिक्षक

स्कूल नंबर 2 के नाम पर रखा गया। वी. मस्किना, क्लाइवलिंस्की जिला, समारा क्षेत्र

सेर्बेवा इरीना अलेक्सेवना

परिचय……………………………………………………3-4

मापदंडों के साथ रैखिक समीकरण और असमानताएँ…………..4-7

द्विघात समीकरण और मापदंडों के साथ असमानताएँ…………7-9

मापदंडों के साथ भिन्नात्मक-तर्कसंगत समीकरण…………..10-11

मापदंडों के साथ तर्कहीन समीकरण और असमानताएँ……11-13

त्रिकोणमितीय समीकरण और मापदंडों के साथ असमानताएँ.14-15

मापदंडों के साथ घातीय समीकरण और असमानताएँ………16-17

लघुगणकीय समीकरण और मापदंडों के साथ असमानताएँ......16-18

एकीकृत राज्य परीक्षा उद्देश्य……………………………………………………18-20

स्वतंत्र कार्य के लिए कार्य…………………………21-28

परिचय।

मापदंडों के साथ समीकरण और असमानताएँ।

यदि किसी समीकरण या असमानता में कुछ गुणांकों को विशिष्ट संख्यात्मक मान नहीं दिया गया है, बल्कि अक्षरों द्वारा निर्दिष्ट किया गया है, तो उन्हें कहा जाता है पैरामीटर,और स्वयं समीकरण या असमानता पैरामीट्रिक.

मापदंडों के साथ किसी समीकरण या असमानता को हल करने के लिए आपको यह करना होगा:

चुनना विशेष अर्थ- यह उस पैरामीटर का मान है जिसमें या जिसके माध्यम से गुजरने पर समीकरण या असमानता का समाधान बदल जाता है।

परिभाषित करना वैध मान- ये उस पैरामीटर के मान हैं जिस पर समीकरण या असमानता समझ में आती है।

किसी समीकरण या असमानता को मापदंडों के साथ हल करने का अर्थ है:

1) निर्धारित करें कि किस पैरामीटर मान पर समाधान मौजूद हैं;

2) पैरामीटर मानों की प्रत्येक स्वीकार्य प्रणाली के लिए, समाधानों का संगत सेट ढूंढें।

आप निम्नलिखित विधियों का उपयोग करके एक पैरामीटर के साथ एक समीकरण को हल कर सकते हैं: विश्लेषणात्मक या ग्राफिकल।

विश्लेषणात्मक विधि इसमें कई मामलों पर विचार करके एक समीकरण का अध्ययन करने का कार्य शामिल है, जिनमें से किसी को भी छोड़ा नहीं जा सकता है।

विश्लेषणात्मक पद्धति का उपयोग करके प्रत्येक प्रकार के मापदंडों के साथ समीकरणों और असमानताओं को हल करने में स्थिति का विस्तृत विश्लेषण और लगातार अनुसंधान शामिल होता है, जिसके दौरान आवश्यकता उत्पन्न होती है "सावधानीपूर्वक संभालना"पैरामीटर के साथ.

ग्राफ़िकल विधि इसमें समीकरण का एक ग्राफ बनाना शामिल है, जिससे कोई यह निर्धारित कर सकता है कि पैरामीटर में परिवर्तन क्रमशः समीकरण के समाधान को कैसे प्रभावित करता है। ग्राफ़ कभी-कभी आपको समस्या को हल करने के लिए विश्लेषणात्मक रूप से आवश्यक और पर्याप्त शर्तें तैयार करने की अनुमति देता है। ग्राफ़िकल समाधान विधि विशेष रूप से प्रभावी होती है जब आपको यह स्थापित करने की आवश्यकता होती है कि पैरामीटर के आधार पर समीकरण की कितनी जड़ें हैं और इसे स्पष्ट रूप से देखने का निस्संदेह लाभ है।

§ 1. रैखिक समीकरण और असमानताएँ।

रेखीय समीकरण ए एक्स = बी , सामान्य रूप में लिखा गया, पैरामीटर के साथ एक समीकरण के रूप में माना जा सकता है, जहां एक्स - अज्ञात , ए , बी - विकल्प. इस समीकरण के लिए, पैरामीटर का विशेष या नियंत्रण मान वह है जिस पर अज्ञात का गुणांक शून्य हो जाता है।

किसी पैरामीटर के साथ रैखिक समीकरण को हल करते समय, उन मामलों पर विचार किया जाता है जब पैरामीटर उसके विशेष मान के बराबर होता है और उससे भिन्न होता है।

विशेष पैरामीटर मान ए मूल्य है ए = 0.

बी = 0 एक विशेष पैरामीटर मान है बी .

पर बी ¹ 0 समीकरण का कोई हल नहीं है.

पर बी = 0 समीकरण इस प्रकार बनेगा: 0x = 0. इस समीकरण का हल कोई भी वास्तविक संख्या है।

स्वरूप की असमानताएँ आह > बी और कुल्हाड़ी < बी (ए ≠ 0)रैखिक असमानताएँ कहलाती हैं। असमानता के समाधान का सेट आह >बी- मध्यान्तर

(; +), अगर ए > 0 , और (-;) , अगर ए< 0 . इसी तरह असमानता के लिए भी

ओह< बी समाधानों का सेट - अंतराल(-;), अगर ए > 0, और (; +), अगर ए< 0.

उदाहरण 1। प्रश्न हल करें कुल्हाड़ी = 5

समाधान: यह एक रैखिक समीकरण है.

अगर ए = 0, फिर समीकरण 0 × एक्स = 5कोई समाधान नहीं है.

अगर ए¹ 0, एक्स =- समीकरण का समाधान.

उत्तर: पर ए¹ 0, एक्स=

a = 0 के लिए कोई समाधान नहीं है।

उदाहरण 2. प्रश्न हल करें कुल्हाड़ी - 6 = 2ए - 3x.

समाधान:यह एक रेखीय समीकरण है, कुल्हाड़ी - 6 = 2ए - 3एक्स (1)

कुल्हाड़ी + 3एक्स = 2ए +6

समीकरण को इस प्रकार पुनः लिखना (ए+3)एक्स = 2(ए+3), दो मामलों पर विचार करें:

ए= -3और ए¹ -3.

अगर ए= -3, फिर कोई वास्तविक संख्या एक्ससमीकरण (1) का मूल है। अगर ए¹ -3 , समीकरण (1) का एक ही मूल है एक्स = 2.

उत्तर:पर ए = -3, एक्स आर ; पर ए ¹ -3, एक्स = 2.

उदाहरण 3. किस पैरामीटर मान पर एसमीकरण की जड़ों के बीच

2एएच - 4ख -ए 2 + 4ए – 4 = 0और भी जड़ें हैं 1 ?

समाधान: आइए समीकरण हल करें 2एएच - 4ख -ए 2 + 4ए – 4 = 0- रेखीय समीकरण

2(ए - 2) एक्स = ए 2 - 4ए +4

2(ए - 2) एक्स = (ए - 2) 2

पर ए = 2समीकरण को हल करना 0x = 0 1 से बड़ी संख्या सहित कोई भी संख्या होगी।

पर ए¹ 2 एक्स =
. शर्त से एक्स > 1, वह है
>1, और >4.

उत्तर:पर ए (2) यू (4;∞).

उदाहरण 4 . प्रत्येक पैरामीटर मान के लिए एसमीकरण के मूलों की संख्या ज्ञात कीजिए आह=8.

समाधान। कुल्हाड़ी = 8- रेखीय समीकरण।

य = ए– क्षैतिज रेखाओं का परिवार;

य = - ग्राफ़ एक अतिपरवलय है. आइए इन फ़ंक्शंस के ग्राफ़ बनाएं।

उत्तर: यदि ए =0, तो समीकरण का कोई हल नहीं है। अगर ए ≠ 0, तो समीकरण का एक हल है।

उदाहरण 5 . ग्राफ़ का उपयोग करके, पता लगाएं कि समीकरण की कितनी जड़ें हैं:

|x| = आह - 1.

y=| एक्स | ,

य = आह - 1- ग्राफ़ एक बिंदु से गुजरने वाली एक सीधी रेखा है (0;-1).

आइए इन फ़ंक्शंस के ग्राफ़ बनाएं।

उत्तर: कब |ए|>1- एक जड़

पर | ए|≤1 – समीकरण की कोई जड़ नहीं है.

उदाहरण 6 . असमानता का समाधान करें कुल्हाड़ी + 4 > 2x + ए 2

समाधान : कुल्हाड़ी + 4 > 2x + ए 2
(ए - 2) एक्स >ए 2 – 4. आइए तीन मामलों पर विचार करें।

उत्तर। एक्स > ए + 2पर ए > 2; एक्स<а + 2, पर ए< 2; पर ए=2कोई समाधान नहीं हैं.

§ 2. द्विघात समीकरण और असमानताएँ

द्विघात समीकरणरूप का एक समीकरण है ओह ² + बी एक्स + सी = 0 , कहाँ ए≠ 0,

ए, बी , साथ - विकल्प.

किसी पैरामीटर के साथ द्विघात समीकरणों को हल करने के लिए, आप निम्नलिखित सूत्रों का उपयोग करके मानक समाधान विधियों का उपयोग कर सकते हैं:

1 ) द्विघात समीकरण का विभेदक: डी = बी ² - 4 एसी , (
²- एसी)

2) द्विघात समीकरण की जड़ों के लिए सूत्र:एक्स 1 =
, एक्स 2 =
,

(एक्स 1,2 =
)

द्विघात असमानताएँ कहलाती हैं

ए एक्स 2 + बी एक्स + सी > 0,ए एक्स 2 + बी एक्स + सी< 0, (1), (2)

ए एक्स 2 + बी एक्स + सी ≥ 0,ए एक्स 2 + बी एक्स + सी ≤ 0,(3), (4)

असमानता (3) के समाधान का सेट असमानता (1) के समाधान के सेट और समीकरण को मिलाकर प्राप्त किया जाता है , ए एक्स 2 + बी एक्स + सी = 0.असमानता के समाधान का सेट (4) इसी तरह पाया जा सकता है।

यदि द्विघात त्रिपद का विभेदक ए एक्स 2 + बी एक्स + सी शून्य से कम है, तो a > 0 के लिए त्रिपद सभी x के लिए धनात्मक है आर.

यदि एक द्विघात त्रिपद की जड़ें (x) हैं 1 < х 2 ), तो a > 0 के लिए यह सेट पर सकारात्मक है(-; एक्स 2 )
(एक्स 2; +) और अंतराल पर नकारात्मक

(एक्स 1; एक्स 2 ). यदि एक< 0, то трехчлен положителен на интервале (х 1 ; एक्स 2 ) और सभी x के लिए नकारात्मक (-; एक्स 1 )
(एक्स 2; +).

उदाहरण 1। प्रश्न हल करें ax² - 2 (a - 1)x - 4 = 0.

यह एक द्विघात समीकरण है

समाधान: विशेष अर्थ ए = 0.

पर ए = 0हमें एक रैखिक समीकरण मिलता है 2x – 4 = 0. इसकी एक ही जड़ होती है एक्स = 2.

पर ए ≠ 0.आइए विवेचक को खोजें।

डी = (a-1)² + 4a = (a+1)²

अगर ए = -1,वह डी = 0 - एक जड़.

आइए प्रतिस्थापित करके मूल ज्ञात करें ए = -1.

-x² + 4x – 4= 0,वह है x² -4x + 4 = 0,हम उसे ढूंढते हैं एक्स=2.

अगर ए ≠ - 1, वह डी >0 . मूल सूत्र का उपयोग करने पर हमें प्राप्त होता है:एक्स=
;

एक्स 1 =2, एक्स 2 = -.

उत्तर:पर a=0 और a= -1समीकरण का एक मूल है एक्स = 2;पर ए ≠ 0 और

ए ≠ - 1 समीकरण के दो मूल हैंएक्स 1 =2, एक्स 2 =-.

उदाहरण 2. इस समीकरण के मूलों की संख्या ज्ञात कीजिए x²-2x-8-a=0पैरामीटर मानों के आधार पर एक।

समाधान। आइए इस समीकरण को इस रूप में फिर से लिखें x²-2x-8=a

य = x²-2x-8- ग्राफ एक परवलय है;

य =ए- क्षैतिज रेखाओं का एक परिवार।

आइए फ़ंक्शंस के ग्राफ़ बनाएं।

उत्तर: कब ए<-9 , समीकरण का कोई समाधान नहीं है; जब a=-9, समीकरण का एक हल होता है; पर ए>-9, समीकरण के दो समाधान हैं।

उदाहरण 3. किस पर एअसमानता (ए - 3) एक्स 2 – 2ax + 3a – 6 >0 x के सभी मानों के लिए धारण करता है?

समाधान।एक द्विघात त्रिपद x यदि के सभी मानों के लिए धनात्मक है

a-3 > 0 और डी<0, т.е. при а, удовлетворяющих системе неравенств

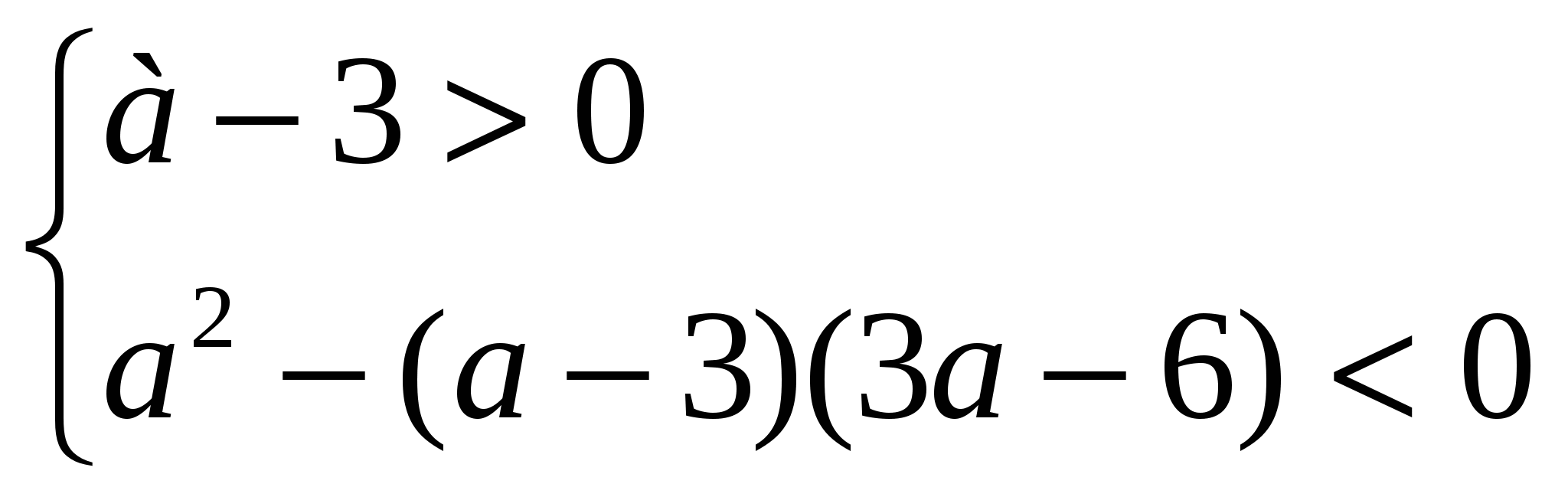
, जहां से यह उसका अनुसरण करता हैए > 6 .

उत्तर।ए > 6

§ 3. पैरामीटर के साथ भिन्नात्मक तर्कसंगत समीकरण,

रैखिक में कम करने योग्य

भिन्नात्मक समीकरणों को हल करने की प्रक्रिया सामान्य योजना के अनुसार की जाती है: समीकरण के दोनों पक्षों को उसके बाएँ और दाएँ पक्षों के सामान्य हर से गुणा करके भिन्न को एक पूर्णांक से बदल दिया जाता है। जिसके बाद बाहरी मूलों को छोड़कर, यानी वे संख्याएँ जो हर को शून्य में बदल देती हैं, पूरा समीकरण हल हो जाता है।

पैरामीटर वाले समीकरणों के मामले में, यह समस्या अधिक जटिल है। यहां, बाहरी जड़ों को "खत्म" करने के लिए, उस पैरामीटर का मान ढूंढना आवश्यक है जो सामान्य विभाजक को शून्य में बदल देता है, यानी पैरामीटर के लिए संबंधित समीकरणों को हल करने के लिए।

उदाहरण 1। प्रश्न हल करें
= 0

समाधान: डी.जेड: एक्स +2 ≠ 0, एक्स ≠ -2

एक्स - ए = 0, एक्स = ए.

उत्तर:पर a ≠ - 2, x=a

पर ए = -2कोई जड़ें नहीं हैं.

उदाहरण 2 . प्रश्न हल करें
-
=
(1)

यह एक भिन्नात्मक परिमेय समीकरण है

समाधान:अर्थ ए = 0विशेष है. पर ए = 0समीकरण का कोई मतलब नहीं है और इसलिए इसकी कोई जड़ें नहीं हैं। अगर ए ≠ 0,तब परिवर्तनों के बाद समीकरण यह रूप लेगा: x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- द्विघात समीकरण।

आइए विवेचक को खोजें = (1 - ए)² - (ए² - 2ए - 3)= 4, समीकरण की जड़ें खोजेंएक्स 1 = ए + 1, एक्स 2 = ए - 3.

समीकरण (1) से समीकरण (2) की ओर बढ़ने पर, समीकरण (1) की परिभाषा का क्षेत्र विस्तारित हो गया, जिससे बाहरी जड़ों की उपस्थिति हो सकती है। इसलिए सत्यापन जरूरी है.

इंतिहान।आइए पाए गए मानों को बाहर करें एक्सजिनमें

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0।

अगर एक्स 1 +1=0, वह है (ए+1) + 1= 0, वह ए=-2.इस प्रकार,

पर ए=-2 , एक्स 1 -

अगर एक्स 1 +2=0, वह है (ए+1)+2=0,वह ए = - 3. इस प्रकार, जब ए = - 3, एक्स 1 - समीकरण का बाह्य मूल. (1).

अगर एक्स 2 +1=0, वह है (ए - 3) + 1= 0, वह ए = 2. इस प्रकार, जब ए = 2 एक्स 2 - समीकरण का बाह्य मूल (1).

अगर एक्स 2 +2=0, वह है ( ए - 3) + 2 = 0,वह ए=1. इस प्रकार, जब ए = 1,

एक्स 2 - समीकरण का बाह्य मूल (1)।

इसके अनुरूप जब ए = - 3हम पाते हैं एक्स = - 3 – 3 = -6;

पर ए = - 2 एक्स = -2 – 3= - 5;

पर ए = 1 एक्स =1 + 1= 2;

पर ए = 2 एक्स = 2+1 = 3.

आप उत्तर लिख सकते हैं.

उत्तर: 1) यदि ए= -3,वह एक्स= -6; 2) यदि ए=-2, वह एक्स= -5; 3) यदि ए= 0, तो कोई जड़ें नहीं हैं ; 4) यदि ए= 1, वह एक्स=2; 5) यदि ए=2, वह एक्स=3; 6) यदि a ≠ -3, a ≠ -2, a ≠ 0, a≠ 1, a ≠ 2, फिर x 1 = ए + 1, एक्स 2 = ए-3.

§4. अपरिमेय समीकरण और असमानताएँ

वे समीकरण एवं असमानताएँ जिनमें चर मूल चिन्ह के नीचे समाहित होता है, कहलाते हैं तर्कहीन.

अपरिमेय समीकरणों को हल करने से समीकरण के दोनों पक्षों को घातांकित करके या एक चर को प्रतिस्थापित करके एक अपरिमेय से तर्कसंगत समीकरण की ओर बढ़ना आता है। जब समीकरण के दोनों पक्षों को एक समान घात तक बढ़ाया जाता है, तो बाहरी जड़ें दिखाई दे सकती हैं। इसलिए, इस पद्धति का उपयोग करते समय, आपको पैरामीटर मानों में परिवर्तन को ध्यान में रखते हुए, पाए गए सभी मूलों को मूल समीकरण में प्रतिस्थापित करके जांचना चाहिए।

रूप का समीकरण
=g (x) सिस्टम के समतुल्य है

असमानता f (x) ≥ 0 समीकरण f (x) = g 2 (x) से अनुसरण करती है।

अपरिमेय असमानताओं को हल करते समय, हम निम्नलिखित समकक्ष परिवर्तनों का उपयोग करेंगे:

≤ जी(एक्स)


≥g(x)

उदाहरण 1। प्रश्न हल करें
= एक्स + 1 (3)

यह एक अपरिमेय समीकरण है

समाधान: अंकगणितीय मूल की परिभाषा के अनुसार, समीकरण (3) प्रणाली के समतुल्य है
.

पर ए = 2सिस्टम के पहले समीकरण का रूप है 0 एक्स = 5यानी इसका कोई समाधान नहीं है.

पर a≠ 2 x=
. आइए जानें किन मूल्यों परए मूल्य मिलाएक्स असमानता को संतुष्ट करता हैएक्स ≥ -1:
≥ - 1,
≥ 0,

कहाँ एक ≤या ए > 2.

उत्तर:पर a≤, a > 2 x=
, पर < а ≤ 2 समीकरण का कोई हल नहीं है.

उदाहरण 2. प्रश्न हल करें
= ए (परिशिष्ट 4)

समाधान। य =

य = ए- क्षैतिज रेखाओं का एक परिवार।

आइए फ़ंक्शंस के ग्राफ़ बनाएं।

उत्तर: पर ए<0 – कोई समाधान नहीं हैं;

पर ए≥ 0 - एक हल।

उदाहरण 3 . आइए असमानता का समाधान करें(ए+1)
<1.

समाधान।ओ.डी.जेड. एक्स ≤ 2. अगर ए+1 ≤0, तो असमानता सभी स्वीकार्य मूल्यों के लिए मान्य है एक्स. अगर ए+1>0, वह

(ए+1)
<1.

<

कहाँ एक्स (2-
2

उत्तर। एक्स (- ;2एक पर (-;-1, एक्स (2-
2

पर ए (-1;+).

§ 5. त्रिकोणमितीय समीकरण और असमानताएँ।

यहां सरलतम त्रिकोणमितीय समीकरणों को हल करने के सूत्र दिए गए हैं:

सिन्क्स = ए
एक्स= (-1)एन आर्कसिन ए+πएन, एन जेड, ≤1, (1)

क्योंकि x = ए
x = ±arccos a + 2 πn, n जेड, ≤1. (2)

अगर >1, तो समीकरण (1) और (2) का कोई हल नहीं है।

टैन एक्स = ए
एक्स= आर्कटैन ए + πएन, एन ज़ेड,ए आर

सीटीजी एक्स = ए
एक्स = आर्कसीटीजी ए + πएन, एन ज़ेड,ए आर

प्रत्येक मानक असमानता के लिए हम समाधानों का सेट दर्शाते हैं:

1. पाप x > ए
आर्क्सिन ए + 2 πn जेड,

पर ए <-1, एक्स आर ; पर ए ≥ 1, कोई समाधान नहीं हैं.

2. . पाप एक्स< a
π - आर्क्सिन ए + 2 πnZ,

a≤-1 के लिए, कोई समाधान नहीं हैं; एक > 1 के लिए,एक्स आर

3. ओल एक्स > ए
- आर्ककोस ए + 2 πn < एक्स < आर्ककोस ए + 2 πn , एन जेड ,

पर ए<-1, एक्स आर ; पर ए ≥ 1 , कोई समाधान नहीं हैं.

4. क्योंकि x आर्ककोस ए+ 2 πnZ,

पर a≤-1 , कोई समाधान नहीं; परए > 1, एक्स आर

5. टैन एक्स > ए, आर्कटैन ए + πnZ

6.टीजी एक्स< a, -π/2 + πn Z

उदाहरण 1। खोजो ए, जिसके लिए इस समीकरण का एक समाधान है:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

समाधान।आइए समीकरण को फॉर्म में लिखें

साथओएस 2 एक्स + (2 ए -4) cosx +(ए – 5)(ए+1) =0,इसे द्विघात के रूप में हल करने पर, हम पाते हैं cosx = 5-एऔर cosx = -ए-1.

समीकरण cosx = 5- ए समाधान उपलब्ध कराए गए हैं -1≤ 5-ए ≤1
4≤ ए≤ 6, और समीकरण। cosx = - एक-1 बशर्ते -1≤ -1-ए ≤ 1
-2 ≤ ए ≤0.

उत्तर। ए -2; 0
4; 6

उदाहरण 2. किस पर बीवहां ऐसी असमानता है
+ बी> 0 सभी x ≠ के लिए मान्य हैπn , एन जेड .

समाधान।चलो रखो ए= 0. असमानता b >0 के लिए है। आइए अब दिखाते हैं कि कोई भी b ≤0 समस्या की शर्तों को पूरा नहीं करता है। वास्तव में, x = लगाना पर्याप्त है π /2, अगर ए <0, и х = - π /2 पर ए ≥0.

उत्तर।बी>0

§ 6. घातीय समीकरण और असमानताएँ

1. समीकरण एच(एक्स) एफ ( एक्स ) = एच(एक्स) जी ( एक्स) पर एच(एक्स) > 0 दो प्रणालियों के संग्रह के बराबर है
और

2. विशेष स्थिति में (h (x)= ए ) समीकरण एएफ(एक्स) = एजी(एक्स) पर ए> 0, दो प्रणालियों के संग्रह के बराबर है

और

3. समीकरण एएफ(एक्स) = बी , कहाँ ए > 0, ए ≠1, बी>0, समीकरण के बराबर

एफ (एक्स) = लॉग ए बी। हो रहा ए=1 को अलग से माना जाता है।

सरलतम चरघातांकीय असमानताओं का समाधान शक्ति गुण पर आधारित है। स्वरूप की असमानताएफ(ए एक्स ) > 0 परिवर्तनीय परिवर्तन का उपयोग करते हुएटी= ए एक्स असमानताओं की प्रणाली को हल करने में कमी आती है
और फिर संबंधित सरल घातीय असमानताओं को हल करने के लिए।

एक गैर-सख्त असमानता को हल करते समय, सख्त असमानता के समाधान के सेट में संबंधित समीकरण की जड़ों को जोड़ना आवश्यक है। जैसा कि अभिव्यक्ति वाले सभी उदाहरणों में समीकरणों को हल करने में होता है एएफ (एक्स), हम मानते हैं ए> 0. मामला ए= 1 को अलग से माना जाता है।

उदाहरण 1 . किस पर एसमीकरण 8 एक्स =
केवल सकारात्मक जड़ें हैं?

समाधान। एक से बड़े आधार वाले घातांकीय फलन के गुण से, हमारे पास x>0 है
8 एक्स >1

>1

>0, कहाँ सेए (1,5;4).

उत्तर। ए (1,5;4).

उदाहरण 2. असमानता का समाधान करें ए 2 ∙2 एक्स > ए

समाधान. आइए तीन मामलों पर विचार करें:

1. ए< 0 . चूँकि असमानता का बायाँ पक्ष सकारात्मक है और दायाँ पक्ष नकारात्मक है, असमानता किसी भी x के लिए मान्य है आर.

2. ए=0. कोई समाधान नहीं हैं.

3. ए > 0 . ए 2 ∙2 एक्स >ए
2 एक्स >
एक्स > -लॉग 2 ए

उत्तर। एक्स आरपर ए > 0; इसका कोई समाधान नहीं है ए =0; एक्स (- लकड़ी का लट्ठा 2 ए; +) परए> 0 .

§ 7. लघुगणकीय समीकरण और असमानताएँ

आइए हम हल करने में प्रयुक्त कुछ तुल्यताएँ प्रस्तुत करें लघुगणकीय समीकरण और असमानताएँ।

1. समीकरण लॉग एफ (एक्स) जी (एक्स) = लॉग एफ (एक्स) एच (एक्स) सिस्टम के बराबर है

विशेषकर, यदि ए >0, ए≠1, फिर

लकड़ी का लट्ठा ए g(x)=लॉग ए एच(एक्स)

2. समीकरण लकड़ी का लट्ठा ए जी(एक्स)=बी
जी(एक्स)=ए बी ( ए >0, एक ≠ 1, जी(x) >0).

3. असमानता लकड़ी का लट्ठा एफ ( एक्स ) जी (एक्स) ≤ लकड़ी का लट्ठा एफ ( एक्स ) एच(एक्स) दो प्रणालियों के संयोजन के बराबर है:
और

यदि एक, b संख्याएँ हैं, a >0, a ≠1, फिर

लकड़ी का लट्ठा ए एफ(एक्स) ≤ बी

लकड़ी का लट्ठा ए एफ(एक्स)>बी

उदाहरण 1। प्रश्न हल करें

समाधान. आइए ODZ खोजें: x > 0, x ≠ ए 4 , ए > 0, ए≠ 1. समीकरण को रूपांतरित करें

लकड़ी का लट्ठा एक्स – 2 = 4 – लकड़ी का लट्ठा ए एक्स
लकड़ी का लट्ठा एक्स + लकड़ी का लट्ठा ए एक्स– 6 = 0, कहाँ से लकड़ी का लट्ठा ए एक्स = - 3

एक्स = ए-3 और लकड़ी का लट्ठा ए एक्स = 2
एक्स = ए 2. शर्त एक्स = ए 4
ए – 3 = ए 4 या ए 2 = ए 4 ODZ पर प्रदर्शन नहीं किया जाता है.

उत्तर:एक्स = ए-3, एक्स = ए 2 बजे ए (0; 1)
(1; ).

उदाहरण 2 . सबसे बड़ा मूल्य ज्ञात करें ए, जिसके लिए समीकरण

2 लकड़ी का लट्ठा -
+ ए = 0 का समाधान है.

समाधान। हम प्रतिस्थापन करेंगे
= टीऔर हमें द्विघात समीकरण 2 मिलता हैटी 2 – टी + ए = 0. हल करने पर हम पाते हैंडी = 1-8 ए . चलो गौर करते हैं डी≥0, 1-8 ए ≥0
ए ≤.

पर ए = द्विघात समीकरण का एक मूल होता हैटी= >0.

उत्तर। ए =

उदाहरण 3 . असमानता का समाधान करेंलकड़ी का लट्ठा(एक्स 2 – 2 एक्स + ए ) > - 3

समाधान। आइए असमानताओं की व्यवस्था को हल करें

वर्ग त्रिपदों के मूल x 1,2 = 1 ±
उनका 3,4 = 1 ±
.

महत्वपूर्ण पैरामीटर मान: ए= 1 और ए= 9.

मान लीजिए कि X 1 और X 2 पहली और दूसरी असमानताओं के समाधान के समुच्चय हैं

एक्स 1
एक्स 2 = एक्स - मूल असमानता का समाधान।

0 पर< ए <1 Х 1 = (- ;1 -
)
(1 +
; +), परए> 1 एक्स 1 = (-;+).

0 पर< ए < 9 Х 2 = (1 -
; 1 +
), परए≥9 X 2 - कोई समाधान नहीं।

आइए तीन मामलों पर विचार करें:

1. 0< ए ≤1 एक्स = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < ए < 9 Х = (1 -
;1 +
).

3. ए≥ 9 एक्स - कोई समाधान नहीं।

एकीकृत राज्य परीक्षा उद्देश्य

उच्च स्तर C1, C2

उदाहरण 1। सभी मान खोजें आर, जिसके लिए समीकरण

आर ∙ सीटीजी 2x+2sinx+ पी= 3 में कम से कम एक जड़ है.

समाधान।आइये समीकरण बदलते हैं

आर ∙ (
- 1) + 2सिंक्स + पी= 3, सिनएक्स =टी, टी
,टी 0.

- पी+2t+ पी = 3, + 2 टी = 3, 3 -2टी = , 3t 2 – 2t 3 = पी .

होने देना एफ(य) = 3 टी 2 – 2 टी 3 . आइए फ़ंक्शन मानों का सेट ढूंढेंएफ(एक्स) पर


. पर / = 6 टी – 6 टी 2 , 6 टी - 6 टी 2 = 0, टी 1 =0, टी 2 = 1. एफ(-1) = 5, एफ(1) = 1.

पर टी
, इ(एफ) =
,

पर टी
, इ(एफ) =
, तभी टी


, इ(एफ) =
.

समीकरण 3 के लिएटी 2 – 2 टी 3 = पी (इसलिए दिए गए) में कम से कम एक जड़ आवश्यक और पर्याप्त थीपी इ(एफ), वह है पी
.

उत्तर।
.

उदाहरण 2.

किस पैरामीटर मान परएसमीकरण लकड़ी का लट्ठा
(4 एक्स 2 – 4 ए + ए 2 +7) = 2 का मूल एक ही है?

समाधान।आइए समीकरण को इसके समतुल्य में बदलें:

4एक्स 2 – 4 ए + ए 2 +7 = (x 2 + 2) 2.

ध्यान दें कि यदि एक निश्चित संख्या x परिणामी समीकरण का मूल है, तो संख्या - x भी इस समीकरण का मूल है। शर्त के अनुसार, यह संभव नहीं है, इसलिए एकमात्र मूल संख्या 0 है।

हम ढूंढ लेंगे ए.

4∙ 0 2 - 4ए + ए 2 +7 = (0 2 + 2) 2 ,

ए 2 - 4ए +7 = 4, ए 2 - 4ए +3 = 0, ए 1 = 1, ए 2 = 3.

इंतिहान।

1) ए 1 = 1. तब समीकरण इस प्रकार दिखता है:लकड़ी का लट्ठा
(4 एक्स 2 +4)=2. आइए इसे सुलझाएं

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 ही एकमात्र मूल है।

2) ए 2 = 3. समीकरण इस प्रकार दिखता है:लकड़ी का लट्ठा
(4 एक्स 2 +4) =2
x = 0 ही एकमात्र मूल है।

उत्तर। 1; 3

उच्च स्तर C4, C5

उदाहरण 3. सभी मान खोजें आर,जिसके लिए समीकरण

एक्स 2 – ( आर+ 3)x + 1= 0 के पूर्णांक मूल हैं और ये मूल असमानता का समाधान हैं: x 3 - 7 आरएक्स 2 + 2एक्स 2 – 14 आरएक्स - 3एक्स +21 आर ≤ 0.

समाधान। चलो एक्स 1, एक्स 2 – समीकरण x के पूर्णांक मूल 2 – (आर + 3)x + 1= 0. फिर, विएटा के सूत्र के अनुसार, समानताएं x 1 + एक्स 2 = आर + 3, एक्स 1 ∙ एक्स 2 = 1. दो पूर्णांकों का गुणनफल x 1 , एक्स 2 केवल दो स्थितियों में एक के बराबर हो सकता है: x 1 = एक्स 2 = 1 या x 1 = एक्स 2 = - 1. यदि x 1 = एक्स 2 = 1, फिरआर + 3 = 1+1 = 2
आर = - 1; यदि एक्स 1 = एक्स 2 = - 1, फिरआर + 3 = - 1 – 1 = - 2
आर = - 5. आइए जाँच करें कि समीकरण की जड़ें x हैं या नहीं 2 – (आर इस असमानता के समाधान द्वारा वर्णित मामलों में + 3)x + 1 = 0। अवसर के लिएआर = - 1, एक्स 1 = एक्स 2 = 1 हमारे पास है

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – सत्य; अवसर के लिए आर= - 5, x 1 = x 2 = - 1 हमारे पास (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – सही। अत: समस्या की शर्तें ही संतुष्ट होती हैं आर=-1 और आर = - 5.

उत्तर।आर 1 =-1 और आर 2 = - 5.

उदाहरण 4. पैरामीटर के सभी सकारात्मक मान ज्ञात करें ए, जिसके लिए संख्या 1 फ़ंक्शन की परिभाषा के क्षेत्र से संबंधित है

पर = (ए
- ए
).

पाठ्यक्रम कार्य

कलाकार: बुग्रोव एस.के.

कई भौतिक प्रक्रियाओं और ज्यामितीय पैटर्न के अध्ययन से अक्सर मापदंडों के साथ समस्याओं का समाधान होता है। कुछ विश्वविद्यालयों में परीक्षा पत्रों में समीकरण, असमानताएं और उनकी प्रणालियाँ भी शामिल होती हैं, जो अक्सर बहुत जटिल होती हैं और समाधान के लिए एक गैर-मानक दृष्टिकोण की आवश्यकता होती है। स्कूल में, स्कूल गणित पाठ्यक्रम के सबसे कठिन खंडों में से एक को केवल कुछ वैकल्पिक कक्षाओं में ही माना जाता है।

इस कार्य को तैयार करने में, मैंने इस विषय के गहन अध्ययन का लक्ष्य निर्धारित किया है, सबसे तर्कसंगत समाधान की पहचान की है जो तुरंत उत्तर की ओर ले जाता है। मेरी राय में, समीकरणों और असमानताओं को मापदंडों के साथ हल करने के लिए ग्राफ़िकल विधि एक सुविधाजनक और तेज़ तरीका है।

मेरा निबंध अक्सर सामने आने वाले प्रकार के समीकरणों, असमानताओं और उनकी प्रणालियों पर चर्चा करता है, और मुझे उम्मीद है कि काम की प्रक्रिया में मैंने जो ज्ञान प्राप्त किया है, वह स्कूल परीक्षा उत्तीर्ण करने और विश्वविद्यालय में प्रवेश करते समय मेरी मदद करेगा।

§ 1. मूल परिभाषाएँ

समीकरण पर विचार करें

¦(ए, बी, सी, …, के, एक्स)=जे(ए, बी, सी, …, के, एक्स), (1)

जहाँ a, b, c, …, k, x परिवर्तनशील राशियाँ हैं।

परिवर्तनशील मानों की कोई भी प्रणाली

a = a0, b = b0, c = c0, …, k = k0, x = x0,

जिसमें इस समीकरण के बाएँ और दाएँ दोनों पक्ष वास्तविक मान लेते हैं, चर a, b, c, ..., k, x के अनुमेय मानों की प्रणाली कहलाती है। मान लीजिए A, a के सभी स्वीकार्य मानों का समुच्चय है, B, b के सभी स्वीकार्य मानों का समुच्चय है, आदि, X, x के सभी स्वीकार्य मानों का समुच्चय है, अर्थात। аОА, bОB, …, xOX। यदि प्रत्येक समुच्चय A, B, C, ..., K के लिए हम क्रमशः एक मान a, b, c, ..., k चुनते हैं और निश्चित करते हैं और उन्हें समीकरण (1) में प्रतिस्थापित करते हैं, तो हमें x के लिए एक समीकरण प्राप्त होता है, अर्थात। एक अज्ञात के साथ समीकरण.

चर a, b, c, ..., k, जिन्हें किसी समीकरण को हल करते समय स्थिर माना जाता है, पैरामीटर कहलाते हैं, और समीकरण को पैरामीटर युक्त समीकरण कहा जाता है।

पैरामीटर लैटिन वर्णमाला के पहले अक्षरों द्वारा निर्दिष्ट हैं: ए, बी, सी, डी, ..., के, एल, एम, एन, और अज्ञात अक्षर x, y, z द्वारा निर्दिष्ट हैं।

मापदंडों के साथ एक समीकरण को हल करने का मतलब यह इंगित करना है कि पैरामीटर समाधान के किन मूल्यों पर मौजूद हैं और वे क्या हैं।

समान पैरामीटर वाले दो समीकरण समतुल्य कहलाते हैं यदि:

ए) वे समान पैरामीटर मानों के लिए समझ में आते हैं;

बी) पहले समीकरण का प्रत्येक समाधान दूसरे का समाधान है और इसके विपरीत।

§ 2. समाधान एल्गोरिथ्म.

समीकरण की परिभाषा का क्षेत्र ज्ञात कीजिए।

हम a को x के एक फलन के रूप में व्यक्त करते हैं।

xOa समन्वय प्रणाली में, हम x के उन मानों के लिए फ़ंक्शन a=¦(x) का एक ग्राफ़ बनाते हैं जो इस समीकरण की परिभाषा के क्षेत्र में शामिल हैं।

हम रेखा a=c के प्रतिच्छेदन बिंदु पाते हैं, जहां cÎ(-¥;+¥) फ़ंक्शन a=¦(x) के ग्राफ के साथ। यदि रेखा a=c ग्राफ a=¦(x) को प्रतिच्छेद करती है , फिर हम प्रतिच्छेदन बिंदुओं का भुज निर्धारित करते हैं। ऐसा करने के लिए, x के लिए समीकरण a=¦(x) को हल करना पर्याप्त है।

हम उत्तर लिखते हैं.

I. समीकरण को हल करें

(1)

चूँकि x=0 समीकरण का मूल नहीं है, इसलिए समीकरण को हल किया जा सकता है:

या

किसी फ़ंक्शन का ग्राफ़ दो "चिपके हुए" हाइपरबोलस हैं। मूल समीकरण के समाधानों की संख्या निर्मित रेखा और सीधी रेखा y=a के प्रतिच्छेदन बिंदुओं की संख्या से निर्धारित होती है।

यदि एक О (-¥;-1]П(1;+¥)П

, तो सीधी रेखा y=a समीकरण (1) के ग्राफ को एक बिंदु पर काटती है। x के लिए समीकरण हल करते समय हम इस बिंदु का भुज ज्ञात करेंगे।

इस प्रकार, इस अंतराल पर, समीकरण (1) का एक हल है

. , तो सीधी रेखा y=a समीकरण (1) के ग्राफ को दो बिंदुओं पर काटती है। इन बिंदुओं का भुज समीकरण और से पाया जा सकता है, हम प्राप्त करते हैं और। , तो रेखा y=a समीकरण (1) के ग्राफ को प्रतिच्छेद नहीं करती है, इसलिए कोई समाधान नहीं है।

यदि एक О (-¥;-1]П(1;+¥)П

, वह ; , वह , ; , तो फिर कोई समाधान नहीं है.

द्वितीय. पैरामीटर ए के सभी मान ज्ञात करें जिसके लिए समीकरण

इसकी तीन अलग-अलग जड़ें हैं।

समीकरण को इस प्रकार पुनः लिखना

और कार्यों की एक जोड़ी की जांच करने पर, आप देख सकते हैं कि पैरामीटर के वांछित मान और केवल वे फ़ंक्शन के ग्राफ़ की उन स्थितियों के अनुरूप होंगे, जिस पर फ़ंक्शन के ग्राफ़ के साथ इसके प्रतिच्छेदन के ठीक तीन बिंदु हैं .

xOy समन्वय प्रणाली में हम फ़ंक्शन का एक ग्राफ़ बनाएंगे

). ऐसा करने के लिए, हम इसे फॉर्म में प्रस्तुत कर सकते हैं और, चार उभरते मामलों पर विचार करने के बाद, हम इस फ़ंक्शन को फॉर्म में लिखते हैं

फ़ंक्शन के ग्राफ़ के बाद से

- यह एक सीधी रेखा है जिसका ऑक्स अक्ष के झुकाव का कोण बराबर है, और निर्देशांक (0, ए) के साथ एक बिंदु पर ओए अक्ष को काटती है, हम निष्कर्ष निकालते हैं कि तीन संकेतित प्रतिच्छेदन बिंदु केवल उस स्थिति में प्राप्त किए जा सकते हैं जब यह रेखा फ़ंक्शन के ग्राफ़ को स्पर्श करती है। इसलिए, हम व्युत्पन्न पाते हैं।

तृतीय. पैरामीटर ए के सभी मान ज्ञात करें, जिनमें से प्रत्येक के लिए समीकरणों की प्रणाली है

समाधान है.

सिस्टम के पहले समीकरण से हमें प्राप्त होता है

इसलिए, यह समीकरण "अर्ध-परवलय" के एक परिवार को परिभाषित करता है - परवलय की दाहिनी शाखाएँ "स्लाइड" होती हैं, जिनके शीर्ष भुज अक्ष के साथ होते हैं।

आइए दूसरे समीकरण के बाईं ओर पूर्ण वर्गों का चयन करें और इसका गुणनखंड करें

विमान के कई बिंदु

दूसरे समीकरण को संतुष्ट करने वाली दो सीधी रेखाएँ हैं और

आइए जानें कि "सेमीपैराबोलस" के परिवार से एक वक्र के पैरामीटर के किन मूल्यों पर परिणामी सीधी रेखाओं में से एक के साथ कम से कम एक सामान्य बिंदु होता है।

श्रृंखला "मापदंडों के साथ समस्याओं को हल करना सीखना"

चतुर्थ. द्विघात समीकरण और पैरामीटर के साथ असमानताएँ

चतुर्थ.1. बुनियादी अवधारणाओं

परिभाषा. फॉर्म (1) का एक फ़ंक्शन, जहां, पैरामीटर के दिए गए फ़ंक्शन हैं ए, परिभाषा के उनके डोमेन के प्रतिच्छेदन पर विचार करते हुए, पैरामीटर के साथ एक द्विघात फ़ंक्शन कहा जाएगा ए.

उदाहरण।

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

परिभाषा. पैरामीटर के साथ द्विघात फ़ंक्शन (1) की परिभाषा का उपडोमेन एहम मानों के जोड़े के पूरे सेट को समझेंगे एक्सऔर एप्रकार ( एक्स; ए), जिनमें से प्रत्येक के लिए अभिव्यक्ति अपना अर्थ नहीं खोती है।

आइए फ़ंक्शन 1-10 की परिभाषा के डोमेन स्थापित करें।

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

यदि पैरामीटर संख्यात्मक मानों में से एक लेता है, तो फ़ंक्शन (1) संख्यात्मक गुणांक वाले फ़ंक्शन में से एक का रूप लेगा:

; ; ;
; ; ; ,

कहाँ क, बी, सी- वास्तविक संख्या।

आइए हम इस तथ्य पर ध्यान दें कि पैरामीटर के कुछ मानों के लिए, एक पैरामीटर के साथ एक द्विघात फ़ंक्शन या तो पैरामीटर के बिना एक द्विघात फ़ंक्शन या एक रैखिक फ़ंक्शन का रूप लेता है।

चूंकि एक पैरामीटर के साथ एक द्विघात फ़ंक्शन अक्सर संख्यात्मक गुणांक के साथ द्विघात या रैखिक कार्यों के एक परिवार को "उत्पन्न" करता है, तो हम इसके बारे में बात कर रहे हैं एक पैरामीटर के साथ द्विघात फ़ंक्शन के ग्राफ़, हमारा मतलब इस परिवार के कई ग्राफ़ से होगा।

परिभाषा. एफॉर्म (1) का एक समीकरण कहा जाता है जहां, पैरामीटर के ये कार्य हैं ए, परिभाषा के उनके डोमेन के प्रतिच्छेदन पर विचार किया जाता है।

विशेष रूप से, कुछ गुणांक या अंतःखंड पद संख्याएँ हो सकते हैं।

उदाहरण।

, (1)
, (2)
, (3)
, (4)
. (5)

एक पैरामीटर के साथ द्विघात फ़ंक्शन की परिभाषा का उपयोग करके, हम एक पैरामीटर के साथ द्विघात समीकरण की निम्नलिखित परिभाषा दे सकते हैं।

परिभाषा. पैरामीटर के साथ द्विघात समीकरण एफॉर्म का एक समीकरण कहा जाता है, जहां पैरामीटर के साथ एक द्विघात फ़ंक्शन होता है ए.

यदि, तो समीकरण (1) पारंपरिक अर्थ में द्विघात है, अर्थात दूसरी उपाधि।
यदि, तो समीकरण (1) रैखिक हो जाता है।

सभी मान्य पैरामीटर मानों के लिए ए, जिसके लिए और ज्ञात सूत्रों का उपयोग करके हम पैरामीटर के संदर्भ में समीकरण (1) की जड़ों के लिए अभिव्यक्ति प्राप्त करते हैं।

वे मूल्य एजिसमें, विशेष मामलों के रूप में अलग से विचार किया जाना चाहिए।
इसलिए, उदाहरण के लिए, समीकरण (5) at का रूप लेता है, जहाँ से।

चतुर्थ.2. पैरामीटर के साथ द्विघात समीकरण

№1. प्रश्न हल करें।

– समीकरण-परिणाम. हम पाते हैं: , ।

समन्वय प्रणाली में ( ओह) हम समाधान पूरा करते हैं। (चित्र .1)

उत्तर: 1. यदि , तो .

2. यदि , तो .

3. यदि , , तो , .

№2. पैरामीटर मान ज्ञात करें ए, जिसमें समीकरण का एक ही मूल है। यदि ऐसे कई मान हैं, तो अपने उत्तर में उनका योग लिखें।

यह समीकरण एक समतुल्य प्रणाली में बदल जाता है:

आइए इसे फॉर्म में लाएं: और इसे समन्वय प्रणाली में ग्राफ़िक रूप से हल करें ( xóa). (अंक 2)।

समीकरण का एक ही मूल है, और।

№3. सभी मान खोजें एक्सजैसे कि पैरामीटर के किसी भी मान के लिए ए, अंतराल (0; 2] से संबंधित नहीं, अभिव्यक्ति अभिव्यक्ति के बराबर नहीं है। (USE-2007)।

आइए समस्या का पुनर्निर्धारण करें: “सभी मान ज्ञात करें एक्सजैसे कि पैरामीटर के किसी भी मान के लिए समीकरण इसकी कोई जड़ नहीं है।"
आइए व्यक्त करें एके माध्यम से एक्स:

1) चलो . तब । इसलिए समीकरण की जड़ें हैं। इसका मतलब यह है कि यह शर्त पूरी नहीं करता.
2) चलो . तब । आइए समन्वय प्रणाली का उपयोग करें ( xóa). (चित्र 3)।

शर्त संतुष्ट है.

№4. पैरामीटर के आधार पर कितनी जड़ें एकोई समीकरण है?

आइए मॉड्यूल का विस्तार करें:

समन्वय प्रणाली में ( xOy) आइए फ़ंक्शन का एक ग्राफ़ बनाएं

और समीकरण द्वारा दी गई समानांतर रेखाओं की एक पेंसिल की कई रेखाएँ। (चित्र 4)।

उत्तर: 1. यदि , तो कोई जड़ें नहीं हैं।

2. यदि , तो एक जड़।

3. यदि , तो दो जड़ें हैं।

चतुर्थ.3. पैरामीटर के साथ द्विघात असमानताएँ

№5. असमानता का समाधान करें .

1 रास्ता.

आइए इसे ध्यान में रखें। फिर किसी के लिए भी इस असमानता का समाधान है बी।(चित्र 5)।

यदि, तो हम असमानता की ओर बढ़ते हैं, जिसके समाधानों का सेट समन्वय प्रणाली में दर्शाया जाएगा ( डिब्बा). (चित्र 6)।

आइए अंजीर को मिलाएं। 5 और 6.

और अब चित्र के अनुसार. 7. इसे खड़ी सीधी रेखाओं से काटने पर उत्तर प्राप्त करना आसान होता है।

उत्तर: 1. यदि , तो .
2. यदि , तो .
3. यदि , तो

विधि 2.

आइए हम समन्वय प्रणाली में असमानता को ग्राफ़िक रूप से हल करें ( xOb):

. (चित्र 8)।

आइए दो मामलों पर विचार करें।

1) . तब असमानता वह रूप ले लेगी जहां .
2) , फिर .

फ़ंक्शन का ग्राफ़ और विमान का वह हिस्सा जिसमें बिंदु हैं जिनके निर्देशांक असमानता को संतुष्ट करते हैं चित्र 8 में दिखाए गए हैं।

1. यदि , तो .
2. यदि , तो . 3. यदि , तो .

3 रास्ता.

आइए अब हम समन्वय प्रणाली में एक ग्राफिकल समाधान प्रस्तुत करें ( xOy). ऐसा करने के लिए, आइए मॉड्यूल का विस्तार करें:

फ़ंक्शन पर विचार करें .

द्विघात त्रिपद की जड़ें .

आइए तुलना करें और.

1) , कहाँ से .

हमें समग्रता प्राप्त होती है। (चित्र 9)

2) , कहाँ से . (चित्र 10)।

फिर यानी .

3) , कहाँ से . (चित्र 11)।

फिर यानी .

उत्तर: 1. यदि , तो .

2. यदि , तो .
3. यदि , तो .

№6. सभी पैरामीटर मान खोजें ए, जिसके लिए फ़ंक्शन का सबसे छोटा मान 2 से अधिक.

यह पैरामीटर के सभी मान ज्ञात करने के लिए पर्याप्त है ए, जिनमें से प्रत्येक के लिए असमानता किसी के लिए सत्य है . आइए असमानता को फॉर्म में फिर से लिखें ., ;

असमानता

(ए, बी, सी,…,, एक्स)>(ए, बी, सी, …, एक्स), (1)

जहां ए, बी, सी,…,- पैरामीटर, और x एक वास्तविक चर है, इसे एक अज्ञात पैरामीटर वाले असमानता कहा जाता है।

पैरामीटर मानों की कोई भी प्रणाली a = a 0 , बी = बी 0 , सी = सी 0 , …, के = के 0 , किसी समारोह के लिए

(ए, बी, सी,…,, एक्स) और

(ए, बी, सी,…,, एक्स

वास्तविक संख्याओं के क्षेत्र में समझ बनाएं, जिसे अनुमेय पैरामीटर मानों की प्रणाली कहा जाता है।

यदि x का वैध मान कहा जाता है

(ए, बी, सी,…,, एक्स) और

(ए, बी, सी,…,, एक्स

पैरामीटर मानों की किसी भी स्वीकार्य प्रणाली के लिए मान्य मान लें।

x के सभी स्वीकार्य मानों के समुच्चय को असमानता की परिभाषा का क्षेत्र (1) कहा जाता है।

एक वास्तविक संख्या x 0 को असमानता का आंशिक समाधान कहा जाता है (1) यदि असमानता है

(ए, बी, सी,…,, एक्स 0 )>(ए, बी, सी,…, एक्स 0 )

अनुमेय पैरामीटर मानों की किसी भी प्रणाली के लिए सत्य है।

असमानता के सभी विशेष समाधानों के समुच्चय (1) को इस असमानता का सामान्य समाधान कहा जाता है।

असमानता को हल करने (1) का अर्थ है यह इंगित करना कि मापदंडों के किन मूल्यों पर एक सामान्य समाधान मौजूद है और वह क्या है।

दो असमानताएँ

(ए, बी, सी,…,, x)>(ए, बी, सी, …, एक्स) और (1)

(ए, बी, सी,…,, एक्स)>(ए, बी, सी, …, एक्स) (2)

समतुल्य कहलाते हैं यदि उनके पास स्वीकार्य पैरामीटर मानों की प्रणालियों के समान सेट के लिए समान सामान्य समाधान हों।

समाधान एल्गोरिथ्म.

हम इस असमानता की परिभाषा का क्षेत्र पाते हैं।

हम असमानता को एक समीकरण में घटा देते हैं।

हम a को x के एक फलन के रूप में व्यक्त करते हैं।

xOa समन्वय प्रणाली में, हम x के उन मानों के लिए फ़ंक्शन a = (x) के ग्राफ़ बनाते हैं जो इस असमानता की परिभाषा के क्षेत्र में शामिल हैं।

हमें ऐसे बिंदुओं के समूह मिलते हैं जो इस असमानता को संतुष्ट करते हैं।

आइए परिणाम पर पैरामीटर के प्रभाव का पता लगाएं।

आइए ग्राफ़ के प्रतिच्छेदन बिंदुओं का भुज खोजें।

आइए एक सीधी रेखा a=const सेट करें और इसे - से + पर स्थानांतरित करें

हम उत्तर लिखते हैं.

यह xOa समन्वय प्रणाली का उपयोग करके मापदंडों के साथ असमानताओं को हल करने के लिए एल्गोरिदम में से एक है। मानक xOy समन्वय प्रणाली का उपयोग करके अन्य समाधान विधियाँ भी संभव हैं।

3. उदाहरण

I. पैरामीटर a के सभी स्वीकार्य मानों के लिए, असमानता को हल करें

पैरामीटर ए की परिभाषा के क्षेत्र में, असमानताओं की प्रणाली द्वारा परिभाषित किया गया है

यह असमानता असमानताओं की प्रणाली के बराबर है

यदि, तो मूल असमानता के समाधान अंतराल को भरते हैं।

उत्तर:, .

द्वितीय. पैरामीटर a के किस मान पर सिस्टम के पास समाधान है?

आइए असमानता के बाईं ओर त्रिपद की जड़ें खोजें -

समानता (*) द्वारा परिभाषित सीधी रेखाएँ निर्देशांक तल aOx को चार क्षेत्रों में विभाजित करती हैं, जिनमें से प्रत्येक में एक वर्ग त्रिपद होता है

एक निरंतर संकेत बनाए रखता है. समीकरण (2) मूल बिंदु पर केन्द्रित त्रिज्या 2 के एक वृत्त को परिभाषित करता है। तब मूल प्रणाली का समाधान छायांकित का प्रतिच्छेदन होगा

एक वृत्त वाला क्षेत्र, जहां और मान सिस्टम से पाए जाते हैं

और मान और सिस्टम से पाए जाते हैं

इन प्रणालियों को हल करते हुए, हम उसे प्राप्त करते हैं

तृतीय. पैरामीटर a के मानों के आधार पर असमानता को हल करें।

हम स्वीकार्य मूल्यों की सीमा पाते हैं -

आइए xOy समन्वय प्रणाली में फ़ंक्शन का एक ग्राफ बनाएं।

जब असमानता का कोई समाधान नहीं है.

जब समाधान के लिए x संबंध को संतुष्ट करता है, जहां

एक पैरामीटर के साथ असमानताओं को हल करना।

असमानताएँ जिनका रूप ax > b, ax है< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются रैखिक असमानताएँ.

एक पैरामीटर के साथ रैखिक असमानताओं को हल करने के सिद्धांत एक पैरामीटर के साथ रैखिक समीकरणों को हल करने के सिद्धांतों के समान हैं।

उदाहरण 1।

असमानता 5x – a > ax + 3 को हल करें।

समाधान।

सबसे पहले, आइए मूल असमानता को बदलें:

5x - ax > a + 3, आइए असमानता के बाईं ओर कोष्ठक से x निकालें:

(5 - ए)x > ए + 3। अब पैरामीटर ए के लिए संभावित मामलों पर विचार करें:

यदि a > 5, तो x< (а + 3) / (5 – а).

यदि a = 5, तो कोई समाधान नहीं है।

यदि एक< 5, то x >(ए + 3) / (5 - ए)।

यह समाधान असमानता का उत्तर होगा.

उदाहरण 2.

a ≠ 1 के लिए असमानता x(a – 2) / (a ​​​ – 1) – 2a/3 ≤ 2x – a को हल करें।

समाधान।

आइए मूल असमानता को बदलें:

x(a – 2) / (a ​​​ – 1) – 2x ≤ 2a/3 – a;

Ах/(а – 1) ≤ -а/3. असमानता के दोनों पक्षों को (-1) से गुणा करने पर, हमें मिलता है:

कुल्हाड़ी/(ए - 1) ≥ ए/3. आइए पैरामीटर ए के लिए संभावित मामलों का पता लगाएं:

1 मामला. मान लीजिए a/(a – 1) > 0 या a € (-∞; 0)ᴗ(1; +∞). फिर x ≥ (a – 1)/3.

केस 2. मान लीजिए a/(a – 1) = 0, अर्थात a = 0. तब x कोई वास्तविक संख्या है।

केस 3. मान लीजिए a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

उत्तर: x € [(ए - 1)/3; +∞) for a € (-∞; 0)ᴗ(1; +∞);
एक्स € ​​[-∞; (ए - 1)/3] एक € (0; 1) के लिए;
x € R के लिए a = 0.

उदाहरण 3.

असमानता को हल करें |1 + x| ≤ एक्स के सापेक्ष कुल्हाड़ी।

समाधान।

यह इस शर्त का अनुसरण करता है कि असमानता कुल्हाड़ी का दाहिना भाग गैर-नकारात्मक होना चाहिए, अर्थात। कुल्हाड़ी ≥ 0. असमानता से मापांक प्रकट करने के नियम द्वारा |1 + x| ≤ कुल्हाड़ी हमारे पास दोहरी असमानता है

कुल्हाड़ी ≤ 1 + x ≤ कुल्हाड़ी. आइए परिणाम को एक सिस्टम के रूप में फिर से लिखें:

(कुल्हाड़ी ≥ 1 + एक्स;
(-ax ≤ 1 + x.

आइए इसे इसमें रूपांतरित करें:

((ए - 1)x ≥ 1;
((ए + 1)एक्स ≥ -1.

हम परिणामी प्रणाली का अंतरालों और बिंदुओं पर अध्ययन करते हैं (चित्र .1):

≤ -1 x € (-∞; 1/(a – 1)] के लिए।

1 पर< а < 0 x € [-1/(а – 1); 1/(а – 1)].

जब a = 0 x = -1.

0 पर< а ≤ 1 решений нет.

असमानताओं को हल करने के लिए ग्राफिकल विधि

ग्राफ़ प्लॉट करने से पैरामीटर वाले समीकरणों को हल करना बहुत सरल हो जाता है। किसी पैरामीटर के साथ असमानताओं को हल करते समय ग्राफिकल विधि का उपयोग करना और भी स्पष्ट और अधिक समीचीन है।

प्रपत्र f(x) ≥ g(x) की असमानताओं को आलेखीय रूप से हल करने का अर्थ है वेरिएबल x के मान ज्ञात करना जिसके लिए फ़ंक्शन f(x) का ग्राफ़ फ़ंक्शन g(x) के ग्राफ़ के ऊपर स्थित है। ऐसा करने के लिए, ग्राफ़ के प्रतिच्छेदन बिंदु (यदि वे मौजूद हैं) ढूंढना हमेशा आवश्यक होता है।

उदाहरण 1।

असमानता को हल करें |x + 5|< bx.

समाधान।

हम फ़ंक्शन y = |x + 5| के ग्राफ़ बनाते हैं और y = bx (अंक 2). असमानता का समाधान वेरिएबल x के वे मान होंगे जिनके लिए फ़ंक्शन का ग्राफ़ y = |x + 5| फ़ंक्शन y = bx के ग्राफ़ के नीचे होगा।

तस्वीर दिखाती है:

1) b > 1 के लिए रेखाएँ प्रतिच्छेद करती हैं। इन फ़ंक्शंस के ग्राफ़ के प्रतिच्छेदन बिंदु का भुज समीकरण x + 5 = bx का समाधान है, जहाँ से x = 5/(b - 1) है। ग्राफ़ y = bx ऊपर अंतराल (5/(b – 1); +∞) से x पर स्थित है, जिसका अर्थ है कि यह सेट असमानता का समाधान है।

2) इसी प्रकार हम इसे -1 पर पाते हैं< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) b ≤ -1 x € (-∞; 5/(b – 1)) के लिए।

4) 0 ≤ b ≤ 1 के लिए, ग्राफ़ प्रतिच्छेद नहीं करते हैं, जिसका अर्थ है कि असमानता का कोई समाधान नहीं है।

उत्तर: x € (-∞; 5/(b – 1)) for b ≤ -1;
x € (-5/(बी + 1); 5/(बी – 1)) -1 पर< b < 0;
0 ≤ b ≤ 1 के लिए कोई समाधान नहीं हैं; x € (5/(b – 1); +∞) b > 1 के लिए।

उदाहरण 2.

असमानता a(a + 1)x > (a + 1)(a + 4) को हल करें।

समाधान।

1) आइए पैरामीटर ए के लिए "नियंत्रण" मान खोजें: ए 1 = 0, और 2 = -1।

2) आइए वास्तविक संख्याओं के प्रत्येक उपसमूह पर इस असमानता को हल करें: (-∞; -1); (-1); (-10); (0); (0; +∞).

ए)ए< -1, из данного неравенства следует, что х >(ए +4)/ए;

बी) ए = -1, तो यह असमानता 0 x > 0 का रूप ले लेगी - कोई समाधान नहीं है;

ग) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, तो इस असमानता का रूप 0 x > 4 है - कोई समाधान नहीं है;

ई) ए > 0, इस असमानता से यह निष्कर्ष निकलता है कि एक्स > (ए + 4)/ए।

उदाहरण 3.

असमानता को हल करें |2 – |x||< a – x.

समाधान।

हम फ़ंक्शन y = |2 – |x|| का एक ग्राफ़ बनाते हैं (चित्र 3)और सीधी रेखा y = -x + a के स्थान के सभी संभावित मामलों पर विचार करें।

उत्तर: असमानता का ≤ -2 के लिए कोई समाधान नहीं है;
x € (-∞; (a – 2)/2) a € (-2; 2] के लिए;
x € (-∞; (a + 2)/2) a > 2 के लिए।

मापदंडों के साथ विभिन्न समस्याओं, समीकरणों और असमानताओं को हल करते समय, बड़ी संख्या में अनुमानी तकनीकों की खोज की जाती है, जिन्हें गणित की किसी भी अन्य शाखा में सफलतापूर्वक लागू किया जा सकता है।

तार्किक सोच और गणितीय संस्कृति के निर्माण में मापदंडों की समस्याएं महत्वपूर्ण भूमिका निभाती हैं। इसीलिए, मापदंडों के साथ समस्याओं को हल करने के तरीकों में महारत हासिल करने के बाद, आप अन्य समस्याओं का सफलतापूर्वक सामना करेंगे।

क्या आपके पास अभी भी प्रश्न हैं? क्या आप नहीं जानते कि असमानताओं को कैसे हल किया जाए?
किसी ट्यूटर से सहायता प्राप्त करने के लिए -.
पहला पाठ निःशुल्क है!

ब्लॉग.साइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, मूल स्रोत के लिंक की आवश्यकता होती है।