त्रिभुज की भुजाओं और ऊँचाइयों का अनुपात। त्रिभुज एबीसी के मूल तत्व. पाइथागोरस प्रमेय को लागू करने में समस्या

ज्यामितीय समस्याओं को हल करते समय, ऐसे एल्गोरिदम का पालन करना उपयोगी होता है। समस्या की शर्तों को पढ़ते समय यह आवश्यक है

• एक चित्र बनाओ. ड्राइंग को यथासंभव समस्या की स्थितियों के अनुरूप होना चाहिए, इसलिए इसका मुख्य कार्य समाधान खोजने में मदद करना है
• समस्या विवरण से सारा डेटा ड्राइंग पर रखें
• समस्या में दिखाई देने वाली सभी ज्यामितीय अवधारणाओं को लिखें
• इन अवधारणाओं से संबंधित सभी प्रमेयों को याद रखें
• चित्र में ज्यामितीय आकृति के तत्वों के बीच सभी संबंध बनाएं जो इन प्रमेयों से अनुसरण करते हैं

उदाहरण के लिए, यदि समस्या में त्रिभुज के कोण के समद्विभाजक शब्द शामिल हैं, तो आपको समद्विभाजक की परिभाषा और गुणों को याद रखना होगा और ड्राइंग में समान या आनुपातिक खंडों और कोणों को इंगित करना होगा।

इस लेख में आपको त्रिभुज के मूल गुण मिलेंगे जिन्हें समस्याओं को सफलतापूर्वक हल करने के लिए जानना आवश्यक है।

त्रिभुज.

एक त्रिभुज का क्षेत्रफल.

1. ,

यहाँ - त्रिभुज की एक मनमाना भुजा, - इस ओर की ऊँचाई कम है।

2. ,

यहाँ और त्रिभुज की मनमानी भुजाएँ हैं, और इन भुजाओं के बीच का कोण है:

3. बगुला का सूत्र:

यहाँ त्रिभुज की भुजाओं की लंबाई है, त्रिभुज का अर्ध-परिधि है,

4. ,

यहाँ त्रिभुज का अर्ध-परिधि है, और अंकित वृत्त की त्रिज्या है।

मान लीजिए स्पर्शरेखा खंडों की लंबाई है।

तब हेरॉन का सूत्र इस प्रकार लिखा जा सकता है:

5.

6. ,

यहाँ - त्रिभुज की भुजाओं की लंबाई, - परिचालित वृत्त की त्रिज्या।

यदि किसी त्रिभुज की भुजा पर एक बिंदु लिया जाता है जो इस भुजा को m:n के अनुपात में विभाजित करता है, तो इस बिंदु को विपरीत कोण के शीर्ष से जोड़ने वाला खंड त्रिभुज को दो त्रिभुजों में विभाजित करता है, जिनके क्षेत्रफल अनुपात में होते हैं एम: एन:

समरूप त्रिभुजों के क्षेत्रफलों का अनुपात समरूपता गुणांक के वर्ग के बराबर होता है।

एक त्रिभुज की माध्यिका

यह त्रिभुज के शीर्ष को विपरीत भुजा के मध्य से जोड़ने वाला एक खंड है।

एक त्रिभुज की माध्यिकाएँएक बिंदु पर प्रतिच्छेद करते हैं और शीर्ष से गिनती करते हुए 2:1 के अनुपात में प्रतिच्छेदन बिंदु से विभाजित होते हैं।

एक नियमित त्रिभुज की माध्यिकाओं का प्रतिच्छेदन बिंदु माध्यिका को दो खंडों में विभाजित करता है, जिनमें से छोटा खंड अंकित वृत्त की त्रिज्या के बराबर होता है, और जिनमें से बड़ा परिचालित वृत्त की त्रिज्या के बराबर होता है।

परिबद्ध वृत्त की त्रिज्या, अंकित वृत्त की त्रिज्या से दोगुनी है: R=2r

माध्यिका लंबाईमनमाना त्रिकोण

,

यहां - भुजा की ओर खींचा गया माध्य - त्रिभुज की भुजाओं की लंबाई।

त्रिभुज का समद्विभाजक

यह त्रिभुज के किसी भी कोण का समद्विभाजक खंड है जो इस कोण के शीर्ष को विपरीत भुजा से जोड़ता है।

त्रिभुज का समद्विभाजकएक भुजा को आसन्न भुजाओं के आनुपातिक खंडों में विभाजित करता है:

एक त्रिभुज के समद्विभाजकएक बिंदु पर प्रतिच्छेद करें, जो अंकित वृत्त का केंद्र है।

कोण के समद्विभाजक के सभी बिंदु कोण की भुजाओं से समान दूरी पर होते हैं।

त्रिभुज की ऊंचाई

यह त्रिभुज के शीर्ष से विपरीत दिशा में गिराया गया एक लंबवत खंड है, या इसकी निरंतरता है। एक अधिक त्रिभुज में, न्यून कोण के शीर्ष से खींची गई ऊँचाई त्रिभुज के बाहर होती है।

किसी त्रिभुज की ऊंचाई एक बिंदु पर प्रतिच्छेद करती है, जिसे कहा जाता है त्रिभुज का लंबकेन्द्र.

एक त्रिभुज की ऊंचाई ज्ञात करने के लिएकिनारे की ओर खींचे जाने पर, आपको किसी भी उपलब्ध तरीके से इसका क्षेत्रफल ज्ञात करना होगा, और फिर सूत्र का उपयोग करना होगा:

त्रिभुज के परिवृत्त का केंद्र, त्रिभुज की भुजाओं पर खींचे गए लंब समद्विभाजक के प्रतिच्छेदन बिंदु पर स्थित है।

त्रिभुज की परिधि त्रिज्या निम्नलिखित सूत्रों का उपयोग करके पाया जा सकता है:

यहां त्रिभुज की भुजाओं की लंबाई है, और त्रिभुज का क्षेत्रफल है।

,

त्रिभुज की भुजा की लंबाई कहां है और विपरीत कोण है। (यह सूत्र साइन प्रमेय से अनुसरण करता है।)

असमानित त्रिकोण

त्रिभुज की प्रत्येक भुजा अन्य दो के योग से कम और अंतर से अधिक है।

किन्हीं दो भुजाओं की लंबाई का योग सदैव तीसरी भुजा की लंबाई से अधिक होता है:

बड़ी भुजा के विपरीत बड़ा कोण होता है; बड़े कोण के विपरीत बड़ी भुजा होती है:

यदि, तो इसके विपरीत.

ज्या का प्रमेय:

त्रिभुज की भुजाएँ सम्मुख कोणों की ज्याओं के समानुपाती होती हैं:

कोसाइन प्रमेय:

किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है, बिना इन भुजाओं के बीच के कोण की कोज्या के गुणनफल के दोगुने के बिना:

सही त्रिकोण

- यह एक त्रिभुज है, जिसका एक कोण 90° है।

एक समकोण त्रिभुज के न्यून कोणों का योग 90° होता है।

कर्ण वह भुजा है जो 90° कोण के विपरीत स्थित होती है। कर्ण सबसे लंबी भुजा है.

पाइथागोरस प्रमेय:

कर्ण का वर्ग पैरों के वर्गों के योग के बराबर होता है:

एक समकोण त्रिभुज में अंकित वृत्त की त्रिज्या बराबर होती है

,

यहाँ अंकित वृत्त की त्रिज्या है, - पैर, - कर्ण:

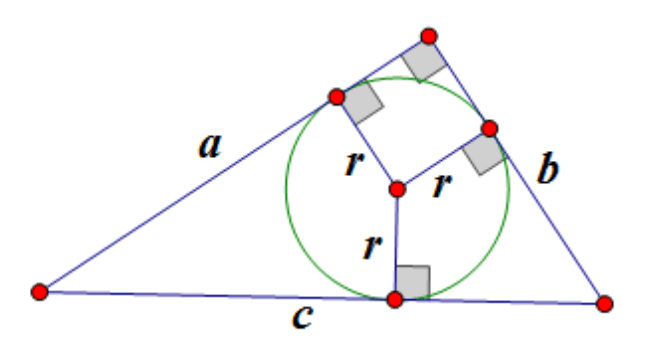
एक समकोण त्रिभुज के परिवृत्त का केंद्र कर्ण के मध्य में स्थित है:

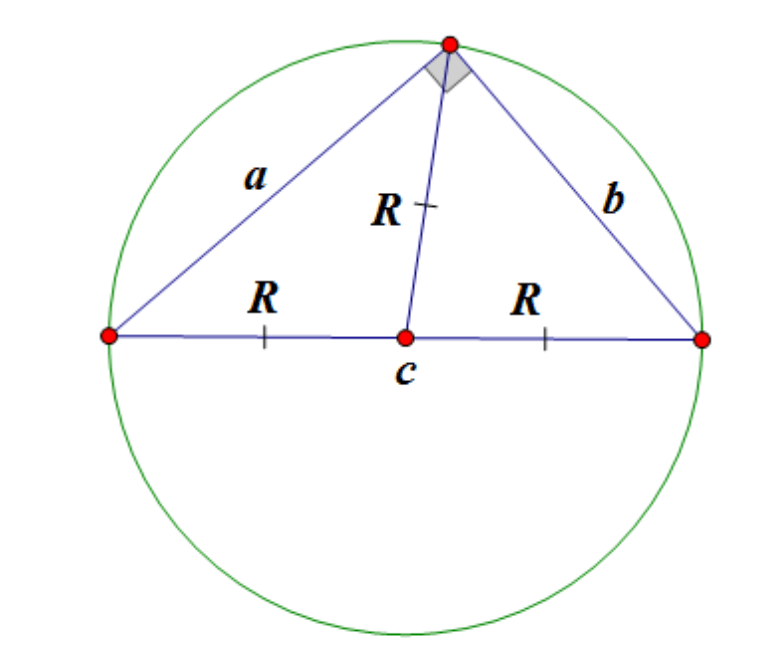
एक समकोण त्रिभुज की माध्यिका कर्ण की ओर खींची गई है, आधे कर्ण के बराबर है।

एक समकोण त्रिभुज की ज्या, कोज्या, स्पर्शज्या और कोटैंजेन्ट की परिभाषादेखना

एक समकोण त्रिभुज में तत्वों का अनुपात:

समकोण के शीर्ष से खींचे गए समकोण त्रिभुज की ऊंचाई का वर्ग कर्ण पर पैरों के प्रक्षेपण के उत्पाद के बराबर है:

पैर का वर्ग कर्ण के गुणनफल और कर्ण पर पैर के प्रक्षेपण के बराबर है:

पैर कोने के विपरीत पड़ा हुआ है आधे कर्ण के बराबर:

समद्विबाहु त्रिकोण।

आधार पर खींचे गए समद्विबाहु त्रिभुज का समद्विभाजक माध्यिका और ऊंचाई है।

समद्विबाहु त्रिभुज में आधार कोण बराबर होते हैं।

शीर्ष कोण.

और - पक्ष,

और - आधार पर कोण.

ऊँचाई, समद्विभाजक और माध्यिका।

ध्यान!किनारे पर खींची गई ऊंचाई, समद्विभाजक और माध्यिका मेल नहीं खाते हैं।

नियमित त्रिकोण

(या समान भुजाओं वाला त्रिकोण ) एक त्रिभुज है, जिसकी सभी भुजाएँ और कोण एक दूसरे के बराबर हैं।

एक नियमित त्रिभुज का क्षेत्रफलके बराबर

त्रिभुज की भुजा की लंबाई कहां है.

एक वृत्त का केंद्र एक नियमित त्रिभुज में अंकित है, एक नियमित त्रिभुज के चारों ओर परिचालित वृत्त के केंद्र के साथ मेल खाता है और माध्यिकाओं के प्रतिच्छेदन बिंदु पर स्थित है।

एक नियमित त्रिभुज की माध्यिकाओं का प्रतिच्छेदन बिंदुमाध्यिका को दो खंडों में विभाजित करता है, जिनमें से छोटा खंड अंकित वृत्त की त्रिज्या के बराबर है, और जो बड़ा है वह परिबद्ध वृत्त की त्रिज्या के बराबर है।

यदि समद्विबाहु त्रिभुज का एक कोण 60° है, तो त्रिभुज नियमित है।

त्रिभुज की मध्य रेखा

यह दो पक्षों के मध्य बिंदुओं को जोड़ने वाला एक खंड है।

चित्र में DE त्रिभुज ABC की मध्य रेखा है।

त्रिभुज की मध्य रेखा तीसरी भुजा के समानांतर और उसके आधे भाग के बराबर है: DE||AC, AC=2DE

त्रिभुज का बाहरी कोण

यह त्रिभुज के किसी भी कोण से सटा हुआ कोण है।

किसी त्रिभुज का बाह्य कोण उसके दो निकटवर्ती कोणों के योग के बराबर होता है।

बाह्य कोण त्रिकोणमितीय कार्य:

त्रिभुजों की समानता के लक्षण:

1 . यदि एक त्रिभुज की दो भुजाएँ और उनके बीच का कोण क्रमशः दूसरे त्रिभुज की दो भुजाओं और उनके बीच के कोण के बराबर हों, तो ऐसे त्रिभुज सर्वांगसम होते हैं।

2 . यदि एक त्रिभुज की एक भुजा और दो आसन्न कोण क्रमशः दूसरे त्रिभुज की एक भुजा और दो आसन्न कोणों के बराबर हों, तो ऐसे त्रिभुज सर्वांगसम होते हैं।

3 यदि एक त्रिभुज की तीन भुजाएँ क्रमशः दूसरे त्रिभुज की तीन भुजाओं के बराबर हों, तो ऐसे त्रिभुज सर्वांगसम होते हैं।

महत्वपूर्ण:चूँकि एक समकोण त्रिभुज में दो कोण स्पष्ट रूप से बराबर होते हैं, इसलिए दो समकोण त्रिभुजों की समानताकेवल दो तत्वों की समानता आवश्यक है: दो भुजाएँ, या एक भुजा और एक न्यूनकोण।

त्रिभुजों की समानता के लक्षण:

1 . यदि एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हों और इन भुजाओं के बीच के कोण बराबर हों, तो ये त्रिभुज समरूप होते हैं।

2 . यदि एक त्रिभुज की तीन भुजाएँ दूसरे त्रिभुज की तीन भुजाओं के समानुपाती हों, तो त्रिभुज समरूप होते हैं।

3 . यदि एक त्रिभुज के दो कोण दूसरे त्रिभुज के दो कोणों के बराबर हों, तो त्रिभुज समरूप होते हैं।

महत्वपूर्ण:समरूप त्रिभुजों में समान भुजाएँ समान कोणों के विपरीत होती हैं।

मेनेलौस का प्रमेय

मान लीजिए कि एक रेखा एक त्रिभुज को प्रतिच्छेद करती है, और यह भुजा के साथ इसके प्रतिच्छेदन का बिंदु है, भुजा के साथ इसके प्रतिच्छेदन का बिंदु है, और भुजा की निरंतरता के साथ इसके प्रतिच्छेदन का बिंदु है। तब

आपकी गोपनीयता बनाए रखना हमारे लिए महत्वपूर्ण है। इस कारण से, हमने एक गोपनीयता नीति विकसित की है जो बताती है कि हम आपकी जानकारी का उपयोग और भंडारण कैसे करते हैं। कृपया हमारी गोपनीयता प्रथाओं की समीक्षा करें और यदि आपके कोई प्रश्न हों तो हमें बताएं।

व्यक्तिगत जानकारी का संग्रहण एवं उपयोग

व्यक्तिगत जानकारी से तात्पर्य उस डेटा से है जिसका उपयोग किसी विशिष्ट व्यक्ति की पहचान करने या उससे संपर्क करने के लिए किया जा सकता है।

जब भी आप हमसे संपर्क करेंगे तो आपसे किसी भी समय आपकी व्यक्तिगत जानकारी प्रदान करने के लिए कहा जा सकता है।

नीचे कुछ उदाहरण दिए गए हैं कि हम किस प्रकार की व्यक्तिगत जानकारी एकत्र कर सकते हैं और हम ऐसी जानकारी का उपयोग कैसे कर सकते हैं।

कौन सी निजी जानकारी हम एकत्र करते हैं:

• जब आप साइट पर कोई आवेदन जमा करते हैं, तो हम आपका नाम, फ़ोन नंबर, ईमेल पता आदि सहित विभिन्न जानकारी एकत्र कर सकते हैं।

हम आपकी व्यक्तिगत जानकारी का उपयोग कैसे करते हैं:

• हमारे द्वारा एकत्र की गई व्यक्तिगत जानकारी हमें अनूठे प्रस्तावों, प्रचारों और अन्य घटनाओं और आगामी कार्यक्रमों के साथ आपसे संपर्क करने की अनुमति देती है।
• समय-समय पर, हम महत्वपूर्ण सूचनाएं और संचार भेजने के लिए आपकी व्यक्तिगत जानकारी का उपयोग कर सकते हैं।
• हम व्यक्तिगत जानकारी का उपयोग आंतरिक उद्देश्यों के लिए भी कर सकते हैं, जैसे कि हमारे द्वारा प्रदान की जाने वाली सेवाओं को बेहतर बनाने और आपको हमारी सेवाओं के संबंध में सिफारिशें प्रदान करने के लिए ऑडिट, डेटा विश्लेषण और विभिन्न शोध करना।
• यदि आप किसी पुरस्कार ड्रा, प्रतियोगिता या इसी तरह के प्रचार में भाग लेते हैं, तो हम ऐसे कार्यक्रमों को संचालित करने के लिए आपके द्वारा प्रदान की गई जानकारी का उपयोग कर सकते हैं।

तृतीय पक्षों को सूचना का प्रकटीकरण

हम आपसे प्राप्त जानकारी को तीसरे पक्ष को प्रकट नहीं करते हैं।

अपवाद:

• यदि आवश्यक हो - कानून, न्यायिक प्रक्रिया के अनुसार, कानूनी कार्यवाही में, और/या सार्वजनिक अनुरोधों या रूसी संघ के क्षेत्र में सरकारी अधिकारियों से अनुरोध के आधार पर - अपनी व्यक्तिगत जानकारी का खुलासा करने के लिए। यदि हम यह निर्धारित करते हैं कि सुरक्षा, कानून प्रवर्तन, या अन्य सार्वजनिक महत्व के उद्देश्यों के लिए ऐसा प्रकटीकरण आवश्यक या उचित है, तो हम आपके बारे में जानकारी का खुलासा भी कर सकते हैं।
• पुनर्गठन, विलय या बिक्री की स्थिति में, हम एकत्र की गई व्यक्तिगत जानकारी को लागू उत्तराधिकारी तीसरे पक्ष को हस्तांतरित कर सकते हैं।

व्यक्तिगत जानकारी की सुरक्षा

हम आपकी व्यक्तिगत जानकारी को हानि, चोरी और दुरुपयोग के साथ-साथ अनधिकृत पहुंच, प्रकटीकरण, परिवर्तन और विनाश से बचाने के लिए - प्रशासनिक, तकनीकी और भौतिक सहित - सावधानियां बरतते हैं।

कंपनी स्तर पर आपकी गोपनीयता का सम्मान करना

यह सुनिश्चित करने के लिए कि आपकी व्यक्तिगत जानकारी सुरक्षित है, हम अपने कर्मचारियों को गोपनीयता और सुरक्षा मानकों के बारे में बताते हैं और गोपनीयता प्रथाओं को सख्ती से लागू करते हैं।

ई ए → ⋅ बी सी → + ई बी → ⋅ सी ए → + ई सी → ⋅ ए बी → = 0 (\displaystyle (\ओवरराइटएरो (ईए))\cdot (\ओवरराइटएरो (बीसी))+(\ओवरराइटएरो (ईबी))\cdot (\ ओवरराइटएरो (CA))+(\ओवरराइटएरो (EC))\cdot (\ओवरराइटएरो (AB))=0)

(पहचान सिद्ध करने के लिए आपको सूत्रों का उपयोग करना चाहिए

एबी → = ई )),\,(\ओवरराइटएरो (बीसी))=(\ओवरराइटएरो (ईसी))-(\ओवरराइटएरो (ईबी)),\,(\ओवरराइटएरो (सीए))=(\ओवरराइटएरो (ईए))-(\ओवरराइटएरो (ईसी)))

बिंदु E को त्रिभुज की दो ऊँचाइयों के प्रतिच्छेदन के रूप में लिया जाना चाहिए।)

• ऑर्थोसेंटरसमकोणीय रूप से केंद्र से संयुग्मित होता है परिवृत्त .
• ऑर्थोसेंटरकेन्द्रक, केन्द्र के समान रेखा पर स्थित है परिवृत्तऔर नौ बिंदुओं के वृत्त का केंद्र (यूलर की सीधी रेखा देखें)।
• ऑर्थोसेंटरएक न्यूनकोण त्रिभुज का केंद्र उसके लंबत्रिकोण में अंकित वृत्त का केंद्र होता है।
• दिए गए त्रिभुज की भुजाओं के मध्य बिंदुओं पर शीर्षों के साथ ऑर्थोसेंटर द्वारा वर्णित त्रिभुज का केंद्र। अंतिम त्रिभुज को पहले त्रिभुज का पूरक त्रिभुज कहा जाता है।
• अंतिम गुण इस प्रकार तैयार किया जा सकता है: त्रिभुज के चारों ओर परिचालित वृत्त का केंद्र कार्य करता है ऑर्थोसेंटरअतिरिक्त त्रिकोण.
• अंक, सममित ऑर्थोसेंटरएक त्रिभुज की भुजाएँ परिवृत्त पर स्थित होती हैं।
• अंक, सममित ऑर्थोसेंटरभुजाओं के मध्य बिंदुओं से संबंधित त्रिभुज भी परिबद्ध वृत्त पर स्थित होते हैं और संबंधित शीर्षों के व्यास के विपरीत बिंदुओं से मेल खाते हैं।
• अगर के बारे मेंतो, परिवृत्त ΔABC का केंद्र है ओ एच → = ओ ए → + ओ बी → + ओ सी → (\displaystyle (\ओवरराइटएरो (ओएच))=(\ओवरराइटएरो (ओए))+(\ओवरराइटएरो (ओबी))+(\ओवरराइटएरो (ओसी))) ,
• त्रिभुज के शीर्ष से लंबकेंद्र तक की दूरी, परिवृत्त के केंद्र से विपरीत दिशा तक की दूरी से दोगुनी है।
• से खींचा गया कोई भी खंड ऑर्थोसेंटरपरिवृत्त के साथ प्रतिच्छेदन से पहले, यह हमेशा यूलर वृत्त द्वारा द्विभाजित होता है। ऑर्थोसेंटरइन दो वृत्तों का समरूपता केंद्र है।
• हैमिल्टन का प्रमेय. लंबकेन्द्र को न्यूनकोण त्रिभुज के शीर्षों से जोड़ने वाले तीन रेखाखंड इसे मूल न्यूनकोण त्रिभुज के समान यूलर वृत्त (नौ बिंदुओं का वृत्त) वाले तीन त्रिभुजों में विभाजित करते हैं।
• हैमिल्टन के प्रमेय के परिणाम:
  • लंबकेन्द्र को न्यूनकोण त्रिभुज के शीर्षों से जोड़ने वाले तीन सीधी रेखा खंड इसे तीन भागों में विभाजित करते हैं हैमिल्टन त्रिकोणपरिबद्ध वृत्तों की समान त्रिज्या वाले।
  • परिबद्ध वृत्तों की त्रिज्याएँ तीन हैं हैमिल्टन त्रिकोणमूल तीव्र त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या के बराबर।
• एक तीव्र त्रिभुज में, लंबकेंद्र त्रिभुज के अंदर स्थित होता है; एक अधिक कोण में - त्रिभुज के बाहर; एक आयताकार में - समकोण के शीर्ष पर।

एक समद्विबाहु त्रिभुज की ऊंचाई के गुण

• यदि किसी त्रिभुज में दो ऊँचाईयाँ समान हैं, तो त्रिभुज समद्विबाहु (स्टाइनर-लेमस प्रमेय) है, और तीसरी ऊँचाई उस कोण की माध्यिका और समद्विभाजक दोनों है जहाँ से वह निकलता है।
• इसका विपरीत भी सत्य है: एक समद्विबाहु त्रिभुज में, दो ऊँचाईयाँ समान होती हैं, और तीसरी ऊँचाई मध्यिका और समद्विभाजक दोनों होती है।
• एक समबाहु त्रिभुज की तीनों ऊँचाइयाँ बराबर होती हैं।

एक त्रिभुज की ऊंचाई के आधारों के गुण

• मैदानऊंचाइयां एक तथाकथित ऑर्थोट्राएंगल बनाती हैं, जिसके अपने गुण होते हैं।
• एक लंबकोण के चारों ओर परिचालित वृत्त यूलर वृत्त है। इस वृत्त में त्रिभुज की भुजाओं के तीन मध्यबिंदु और लंबकेंद्र को त्रिभुज के शीर्षों से जोड़ने वाले तीन खंडों के तीन मध्यबिंदु भी शामिल हैं।
• अंतिम संपत्ति का एक और सूत्रीकरण:
  • नौ-बिंदु वृत्त के लिए यूलर का प्रमेय. मैदानतीन ऊंचाइयोंमनमाना त्रिभुज, इसकी तीन भुजाओं के मध्यबिंदु ( इसके आंतरिक की नींवमाध्यिकाएँ) और इसके शीर्षों को लंबकेंद्र से जोड़ने वाले तीन खंडों के मध्यबिंदु, सभी एक ही वृत्त पर स्थित हैं (पर) नौ बिंदु वृत्त).
• प्रमेय. किसी भी त्रिभुज में जोड़ने वाला खंड मैदानदो ऊंचाइयोंत्रिभुज, दिए गए त्रिभुज के समान एक त्रिभुज काटता है।
• प्रमेय. एक त्रिभुज में, जोड़ने वाला खंड मैदानदो ऊंचाइयोंदो भुजाओं पर स्थित त्रिभुज antiparallelकिसी तीसरे पक्ष के साथ जिसके साथ उसका कोई साझा आधार नहीं है। एक वृत्त हमेशा इसके दोनों सिरों के माध्यम से, साथ ही उल्लिखित तीसरी भुजा के दो शीर्षों के माध्यम से भी खींचा जा सकता है।

त्रिभुज ऊंचाई के अन्य गुण

त्रिभुज की न्यूनतम ऊँचाई के गुण

किसी त्रिभुज की न्यूनतम ऊँचाई में कई चरम गुण होते हैं। उदाहरण के लिए:

• त्रिभुज के तल में स्थित रेखाओं पर त्रिभुज के न्यूनतम ओर्थोगोनल प्रक्षेपण की लंबाई इसकी सबसे छोटी ऊंचाई के बराबर होती है।
• किसी समतल में न्यूनतम सीधा कट जिसके माध्यम से एक कठोर त्रिकोणीय प्लेट को खींचा जा सकता है, उसकी लंबाई इस प्लेट की सबसे छोटी ऊंचाई के बराबर होनी चाहिए।
• त्रिभुज की परिधि के साथ दो बिंदुओं की एक दूसरे की ओर निरंतर गति के साथ, पहली बैठक से दूसरी बैठक तक गति के दौरान उनके बीच की अधिकतम दूरी त्रिभुज की सबसे छोटी ऊंचाई की लंबाई से कम नहीं हो सकती है।
• किसी त्रिभुज की न्यूनतम ऊंचाई हमेशा उस त्रिभुज के भीतर होती है।

बुनियादी रिश्ते

• h a = b पाप ⁡ γ = c पाप ⁡ β , (\displaystyle h_(a)=b\sin \गामा =c\sin \beta ,)
• h a = 2 S a , (\displaystyle h_(a)=(\frac (2S)(a)),)कहाँ एस (\डिस्प्लेस्टाइल एस)- एक त्रिभुज का क्षेत्रफल, ए (\डिस्प्लेस्टाइल ए)- त्रिभुज की भुजा की लंबाई जिससे ऊँचाई कम हो जाती है।
• h a 2 = 1 2 (b 2 + c 2 − 1 2 (a 2 + (b 2 − c 2) 2 a 2)) (\displaystyle h_(a)^(2)=(\frac (1)(2) ))(b^(2)+c^(2)-(\frac (1)(2))(a^(2)+(\frac ((b^(2)-c^(2))^ (2))(ए^(2))))))
• h a = b c 2 R , (\displaystyle h_(a)=(\frac (bc)(2R)),)कहाँ बी सी (\डिस्प्लेस्टाइल बीसी)- पक्षों का उत्पाद, आर − (\डिस्प्लेस्टाइल आर-)परिधि
• h a: h b: h c = 1 a: 1 b: 1 c = b c: a c: a b (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):( \frac (1)(b)):(\frac (1)(c))=bc:ac:ab)
• 1 h a + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (सी)))=(\frac (1)(r))), कहाँ आर (\डिस्प्लेस्टाइल आर)- अंकित वृत्त की त्रिज्या.
• एस = 1 (1 एच ए + 1 एच बी + 1 एच सी) ⋅ (1 एच ए + 1 एच बी - 1 एच सी) ⋅ (1 एच ए + 1 एच सी - 1 एच बी) ⋅ (1 एच बी + 1 एच सी - 1 एच ए) (\डिस्प्लेस्टाइल एस =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c) ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), कहाँ एस (\डिस्प्लेस्टाइल एस)- एक त्रिभुज का क्षेत्रफल.
• ए = 2 एच ए ⋅ (1 एच ए + 1 एच बी + 1 एच सी) ⋅ (1 एच ए + 1 एच बी - 1 एच सी) ⋅ (1 एच ए + 1 एच सी - 1 एच बी) ⋅ (1 एच बी + 1 एच सी - 1 एच ए) (\ डिस्प्लेस्टाइल a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c)))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1) )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (ए))))))))), ए (\डिस्प्लेस्टाइल ए)- त्रिभुज की वह भुजा जिस पर ऊँचाई उतरती है h a (\displaystyle h_(a)).
• एक समद्विबाहु त्रिभुज की ऊंचाई आधार से कम की गई: h c = 1 2 4 a 2 - c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\sqrt (4a^(2)-c^(2))),)

कहाँ सी (\डिस्प्लेस्टाइल सी)- आधार, ए (\डिस्प्लेस्टाइल ए)- ओर।

समकोण त्रिभुज ऊंचाई प्रमेय

यदि समकोण त्रिभुज में ऊँचाई है ए बी सी (\डिस्प्लेस्टाइल एबीसी)लंबाई एच (\डिस्प्लेस्टाइल एच)एक समकोण के शीर्ष से खींचा गया, कर्ण को लंबाई से विभाजित करता है सी (\डिस्प्लेस्टाइल सी)खंडों में एम (\डिस्प्लेस्टाइल एम)और एन (\डिस्प्लेस्टाइल एन), पैरों के अनुरूप बी (\डिस्प्लेस्टाइल बी)और ए (\डिस्प्लेस्टाइल ए), तो निम्नलिखित समानताएँ सत्य हैं।

त्रिभुज) या त्रिभुज के बाहर एक अधिक त्रिभुज पर गुजरें।

विश्वकोश यूट्यूब

1 / 5

✪ ऊँचाई, त्रिभुज ग्रेड 7 का माध्य समद्विभाजक

✪ त्रिभुज का समद्विभाजक, माध्यिका, ऊँचाई। ज्यामिति 7वीं कक्षा

✪ ग्रेड 7, पाठ 17, एक त्रिभुज की माध्यिकाएँ, समद्विभाजक और शीर्षलंब

✪ त्रिभुज की माध्यिका, समद्विभाजक, ऊँचाई | ज्यामिति

✪ समद्विभाजक की लंबाई, माध्यिका और ऊंचाई कैसे ज्ञात करें? | मेरे साथ बेवकूफ #031 | बोरिस ट्रुशिन

उपशीर्षक

एक त्रिभुज की तीन ऊँचाइयों के प्रतिच्छेदन बिंदु के गुण (लंबकेन्द्र)

ई ए → ⋅ बी सी → + ई बी → ⋅ सी ए → + ई सी → ⋅ ए बी → = 0 (\displaystyle (\ओवरराइटएरो (ईए))\cdot (\ओवरराइटएरो (बीसी))+(\ओवरराइटएरो (ईबी))\cdot (\ ओवरराइटएरो (CA))+(\ओवरराइटएरो (EC))\cdot (\ओवरराइटएरो (AB))=0)

(पहचान सिद्ध करने के लिए आपको सूत्रों का उपयोग करना चाहिए

एबी → = ई )),\,(\ओवरराइटएरो (बीसी))=(\ओवरराइटएरो (ईसी))-(\ओवरराइटएरो (ईबी)),\,(\ओवरराइटएरो (सीए))=(\ओवरराइटएरो (ईए))-(\ओवरराइटएरो (ईसी)))

बिंदु E को त्रिभुज की दो ऊँचाइयों के प्रतिच्छेदन के रूप में लिया जाना चाहिए।)

• ऑर्थोसेंटरसमकोणीय रूप से केंद्र से संयुग्मित होता है परिबद्ध घेरा .
• ऑर्थोसेंटरकेन्द्रक, केन्द्र के समान रेखा पर स्थित है परिवृत्तऔर नौ बिंदुओं वाले एक वृत्त का केंद्र (यूलर की सीधी रेखा देखें)।
• ऑर्थोसेंटरएक न्यूनकोण त्रिभुज का केंद्र उसके लंबत्रिकोण में अंकित वृत्त का केंद्र होता है।
• दिए गए त्रिभुज की भुजाओं के मध्य बिंदुओं पर शीर्षों के साथ ऑर्थोसेंटर द्वारा वर्णित त्रिभुज का केंद्र। अंतिम त्रिभुज को पहले त्रिभुज का पूरक त्रिभुज कहा जाता है।
• अंतिम गुण इस प्रकार तैयार किया जा सकता है: त्रिभुज के चारों ओर परिचालित वृत्त का केंद्र कार्य करता है ऑर्थोसेंटरअतिरिक्त त्रिकोण.
• अंक, सममित ऑर्थोसेंटरएक त्रिभुज की भुजाएँ परिवृत्त पर स्थित होती हैं।
• अंक, सममित ऑर्थोसेंटरभुजाओं के मध्य बिंदुओं से संबंधित त्रिभुज भी परिबद्ध वृत्त पर स्थित होते हैं और संबंधित शीर्षों के व्यास के विपरीत बिंदुओं से मेल खाते हैं।
• यदि O परिवृत्त ΔABC का केंद्र है, तो ओ एच → = ओ ए → + ओ बी → + ओ सी → (\displaystyle (\ओवरराइटएरो (ओएच))=(\ओवरराइटएरो (ओए))+(\ओवरराइटएरो (ओबी))+(\ओवरराइटएरो (ओसी))) ,
• त्रिभुज के शीर्ष से लंबकेंद्र तक की दूरी, परिवृत्त के केंद्र से विपरीत दिशा तक की दूरी से दोगुनी है।
• से खींचा गया कोई भी खंड ऑर्थोसेंटरपरिवृत्त के साथ प्रतिच्छेद करने से पहले, इसे हमेशा यूलर सर्कल द्वारा आधे में विभाजित किया जाता है। ऑर्थोसेंटरइन दो वृत्तों का समरूपता केंद्र है।
• हैमिल्टन का प्रमेय. एक न्यूनकोण त्रिभुज के शीर्षों के साथ लंबकेंद्र को जोड़ने वाले तीन सीधी रेखा खंड इसे मूल न्यूनकोण त्रिभुज के समान यूलर वृत्त (नौ बिंदुओं का वृत्त) वाले तीन त्रिभुजों में विभाजित करते हैं।
• हैमिल्टन के प्रमेय के परिणाम:
  • लंबकेन्द्र को न्यूनकोण त्रिभुज के शीर्षों से जोड़ने वाले तीन सीधी रेखा खंड इसे तीन भागों में विभाजित करते हैं हैमिल्टन त्रिकोणपरिबद्ध वृत्तों की समान त्रिज्या वाले।
  • परिबद्ध वृत्तों की त्रिज्याएँ तीन हैं हैमिल्टन त्रिकोणमूल तीव्र त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या के बराबर।
• एक तीव्र त्रिभुज में, लंबकेंद्र त्रिभुज के अंदर स्थित होता है; एक अधिक कोण में - त्रिभुज के बाहर; एक आयताकार में - समकोण के शीर्ष पर।

एक समद्विबाहु त्रिभुज की ऊंचाई के गुण

• यदि किसी त्रिभुज में दो ऊँचाईयाँ समान हैं, तो त्रिभुज समद्विबाहु (स्टाइनर-लेमस प्रमेय) है, और तीसरी ऊँचाई उस कोण की माध्यिका और समद्विभाजक दोनों है जहाँ से वह निकलता है।
• इसका विपरीत भी सत्य है: एक समद्विबाहु त्रिभुज में, दो ऊँचाईयाँ समान होती हैं, और तीसरी ऊँचाई मध्यिका और समद्विभाजक दोनों होती है।
• एक समबाहु त्रिभुज की तीनों ऊँचाइयाँ बराबर होती हैं।

एक त्रिभुज की ऊंचाई के आधारों के गुण

• मैदानऊंचाइयां एक तथाकथित ऑर्थोट्राएंगल बनाती हैं, जिसके अपने गुण होते हैं।
• एक लंबकोण के चारों ओर परिचालित वृत्त यूलर वृत्त है। इस वृत्त में त्रिभुज की भुजाओं के तीन मध्यबिंदु और लंबकेंद्र को त्रिभुज के शीर्षों से जोड़ने वाले तीन खंडों के तीन मध्यबिंदु भी शामिल हैं।
• अंतिम संपत्ति का एक और सूत्रीकरण:
  • नौ बिंदुओं के एक वृत्त के लिए यूलर का प्रमेय. मैदानतीन ऊंचाइयोंमनमाना त्रिभुज, इसकी तीन भुजाओं के मध्यबिंदु ( इसके आंतरिक की नींवमाध्यिकाएँ) और इसके शीर्षों को लंबकेंद्र से जोड़ने वाले तीन खंडों के मध्यबिंदु, सभी एक ही वृत्त पर स्थित हैं (पर) नौ बिंदु वृत्त).
• प्रमेय. किसी भी त्रिभुज में जोड़ने वाला खंड मैदानदो ऊंचाइयोंत्रिभुज, दिए गए त्रिभुज के समान एक त्रिभुज काटता है।
• प्रमेय. एक त्रिभुज में, जोड़ने वाला खंड मैदानदो ऊंचाइयोंदो भुजाओं पर स्थित त्रिभुज antiparallelकिसी तीसरे पक्ष के साथ जिसके साथ उसका कोई साझा आधार नहीं है। एक वृत्त हमेशा इसके दोनों सिरों के माध्यम से, साथ ही उल्लिखित तीसरी भुजा के दो शीर्षों के माध्यम से भी खींचा जा सकता है।

त्रिभुज ऊंचाई के अन्य गुण

• यदि एक त्रिभुज बहुमुखी (विषम भुज तथ कोण वाला), तो यह आंतरिककिसी शीर्ष से खींचा गया समद्विभाजक किसके बीच स्थित होता है? आंतरिकमाध्यिका और ऊँचाई एक ही शीर्ष से खींची गई।
• एक त्रिभुज की ऊंचाई समकोणीय रूप से व्यास (त्रिज्या) से संयुग्मित होती है परिबद्ध घेरा, एक ही शीर्ष से खींचा गया।
• एक न्यूनकोण त्रिभुज में दो होते हैं ऊंचाइयोंइसमें से समरूप त्रिभुजों को काट लें।
• एक समकोण त्रिभुज में ऊंचाई, एक समकोण के शीर्ष से खींचा गया, इसे मूल के समान दो त्रिभुजों में विभाजित करता है।

त्रिभुज की न्यूनतम ऊँचाई के गुण

किसी त्रिभुज की न्यूनतम ऊँचाई में कई चरम गुण होते हैं। उदाहरण के लिए:

• त्रिभुज के तल में स्थित रेखाओं पर त्रिभुज के न्यूनतम ओर्थोगोनल प्रक्षेपण की लंबाई इसकी सबसे छोटी ऊंचाई के बराबर होती है।
• किसी समतल में न्यूनतम सीधा कट जिसके माध्यम से एक कठोर त्रिकोणीय प्लेट को खींचा जा सकता है, उसकी लंबाई इस प्लेट की सबसे छोटी ऊंचाई के बराबर होनी चाहिए।
• त्रिभुज की परिधि के साथ दो बिंदुओं की एक दूसरे की ओर निरंतर गति के साथ, पहली बैठक से दूसरी बैठक तक गति के दौरान उनके बीच की अधिकतम दूरी त्रिभुज की सबसे छोटी ऊंचाई की लंबाई से कम नहीं हो सकती है।
• किसी त्रिभुज की न्यूनतम ऊंचाई हमेशा उस त्रिभुज के भीतर होती है।

बुनियादी रिश्ते

• एच ए = बी ⋅ पाप ⁡ γ = सी ⋅ पाप ⁡ β , (\displaystyle h_(a)=b(\cdot )\sin \gamma =c(\cdot )\sin \beta ,)
• h a = 2 ⋅ S a , (\displaystyle h_(a)=(\frac (2(\cdot )S)(a)),)कहाँ एस (\डिस्प्लेस्टाइल एस)- एक त्रिभुज का क्षेत्रफल, ए (\डिस्प्लेस्टाइल ए)- त्रिभुज की भुजा की लंबाई जिससे ऊँचाई कम हो जाती है।
• h a = b ⋅ c 2 ⋅ R , (\displaystyle h_(a)=(\frac (b(\cdot )c)(2(\cdot )R)),)कहाँ b ⋅ c (\displaystyle b(\cdot )c)- पक्षों का उत्पाद, आर − (\डिस्प्लेस्टाइल आर-)परिधि
• h a: h b: h c = 1 a: 1 b: 1 c = (b ⋅ c) : (a ⋅ c) : (a ⋅ b) . (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):(\frac (1)(b)):(\frac (1)(c)) =(b(\cdot )c):(a(\cdot )c):(a(\cdot )b).)
• 1 h a + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (सी)))=(\frac (1)(r))), कहाँ आर (\डिस्प्लेस्टाइल आर)- अंकित वृत्त की त्रिज्या.
• एस = 1 (1 एच ए + 1 एच बी + 1 एच सी) ⋅ (1 एच ए + 1 एच बी - 1 एच सी) ⋅ (1 एच ए + 1 एच सी - 1 एच बी) ⋅ (1 एच बी + 1 एच सी - 1 एच ए) (\डिस्प्लेस्टाइल एस =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c) ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), कहाँ एस (\डिस्प्लेस्टाइल एस)- एक त्रिभुज का क्षेत्रफल.
• ए = 2 एच ए ⋅ (1 एच ए + 1 एच बी + 1 एच सी) ⋅ (1 एच ए + 1 एच बी - 1 एच सी) ⋅ (1 एच ए + 1 एच सी - 1 एच बी) ⋅ (1 एच बी + 1 एच सी - 1 एच ए) (\ डिस्प्लेस्टाइल a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c)))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1) )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (ए))))))))), ए (\डिस्प्लेस्टाइल ए)- त्रिभुज की वह भुजा जिस पर ऊँचाई उतरती है h a (\displaystyle h_(a)).
• एक समद्विबाहु त्रिभुज की ऊंचाई आधार से कम की गई: h c = 1 2 ⋅ 4 a 2 - c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\cdot )(\sqrt (4a^(2)-c^(2)) ),)

कहाँ सी (\डिस्प्लेस्टाइल सी)- आधार, ए (\डिस्प्लेस्टाइल ए)- ओर।

समकोण त्रिभुज ऊंचाई प्रमेय

यदि एक समकोण त्रिभुज ABC में ऊँचाई लंबाई की है एच (\डिस्प्लेस्टाइल एच)एक समकोण के शीर्ष से खींचा गया, कर्ण को लंबाई से विभाजित करता है सी (\डिस्प्लेस्टाइल सी)खंडों में एम (\डिस्प्लेस्टाइल एम)और एन (\डिस्प्लेस्टाइल एन), पैरों के अनुरूप बी (\डिस्प्लेस्टाइल बी)और ए (\डिस्प्लेस्टाइल ए), तो निम्नलिखित समानताएँ सत्य हैं।

वीडियो पाठ्यक्रम "गेट एन ए" में 60-65 अंकों के साथ गणित में एकीकृत राज्य परीक्षा को सफलतापूर्वक उत्तीर्ण करने के लिए आवश्यक सभी विषय शामिल हैं। गणित में प्रोफ़ाइल एकीकृत राज्य परीक्षा के सभी कार्य 1-13 पूर्णतः। गणित में बेसिक यूनिफाइड स्टेट परीक्षा उत्तीर्ण करने के लिए भी उपयुक्त। यदि आप 90-100 अंकों के साथ एकीकृत राज्य परीक्षा उत्तीर्ण करना चाहते हैं, तो आपको भाग 1 को 30 मिनट में और गलतियों के बिना हल करना होगा!

ग्रेड 10-11 के साथ-साथ शिक्षकों के लिए एकीकृत राज्य परीक्षा के लिए तैयारी पाठ्यक्रम। गणित में एकीकृत राज्य परीक्षा के भाग 1 (पहली 12 समस्याएं) और समस्या 13 (त्रिकोणमिति) को हल करने के लिए आपको जो कुछ भी चाहिए वह सब कुछ। और यह एकीकृत राज्य परीक्षा में 70 अंक से अधिक है, और न तो 100 अंक वाला छात्र और न ही मानविकी का छात्र इनके बिना कर सकता है।

सभी आवश्यक सिद्धांत. एकीकृत राज्य परीक्षा के त्वरित समाधान, नुकसान और रहस्य। FIPI टास्क बैंक से भाग 1 के सभी मौजूदा कार्यों का विश्लेषण किया गया है। पाठ्यक्रम पूरी तरह से एकीकृत राज्य परीक्षा 2018 की आवश्यकताओं का अनुपालन करता है।

पाठ्यक्रम में 5 बड़े विषय हैं, प्रत्येक विषय 2.5 घंटे का है। प्रत्येक विषय प्रारंभ से, सरल और स्पष्ट रूप से दिया गया है।

सैकड़ों एकीकृत राज्य परीक्षा कार्य। शब्द समस्याएँ और संभाव्यता सिद्धांत। समस्याओं को हल करने के लिए सरल और याद रखने में आसान एल्गोरिदम। ज्यामिति। सिद्धांत, संदर्भ सामग्री, सभी प्रकार के एकीकृत राज्य परीक्षा कार्यों का विश्लेषण। स्टीरियोमेट्री। पेचीदा समाधान, उपयोगी चीट शीट, स्थानिक कल्पना का विकास। खरोंच से समस्या तक त्रिकोणमिति 13. रटने के बजाय समझना। जटिल अवधारणाओं की स्पष्ट व्याख्या. बीजगणित. मूल, घात और लघुगणक, कार्य और व्युत्पन्न। एकीकृत राज्य परीक्षा के भाग 2 की जटिल समस्याओं को हल करने का आधार।