Улсын төсвийн боловсролын байгууллага

Самара мужийн дунд ерөнхий боловсрол

нэрэмжит 2-р сургууль. V. Маскина төмөр зам Урлаг. Клявлино

Клявлинскийн хотын дүүрэг

Самара муж

«Тэгшитгэл

Тэгээд

тэгш бус байдал

параметрүүдтэй"

заавар

Клявлино

Заавар

"Параметр бүхий тэгшитгэл ба тэгш бус байдал" 10-11-р ангийн сурагчдад зориулсан

Энэхүү гарын авлага нь хөндлөнгийн шалгалтанд тэнцсэн "Параметр бүхий тэгшитгэл ба тэгш бус байдал" сонгох хичээлийн хөтөлбөрийн хавсралт юм (Самар мужийн Боловсрол, шинжлэх ухааны яамны шинжлэх ухаан, арга зүйн шинжээчдийн зөвлөлийн 2008 оны 12-р сарын 19-ний өдрийн зөвлөмж). Самара мужийн боловсролын байгууллагуудад ашиглах)

Зохиогчид

Ромаданова Ирина Владимировна

Клявлинская нэрэмжит дунд боловсролын сургуулийн математикийн багш

нэрэмжит 2-р сургууль. В. Маскина, Самара мужийн Клявлинский дүүрэг

Сербаева Ирина Алексеевна

Танилцуулга………………………………………………………………3-4

Параметртэй шугаман тэгшитгэл ба тэгш бус байдал……………..4-7

Параметртэй квадрат тэгшитгэл ба тэгш бус байдал……………7-9

Параметртэй бутархай-рационал тэгшитгэл……………..10-11

Параметртэй иррационал тэгшитгэл ба тэгш бус байдал……11-13

Тригонометрийн тэгшитгэл ба параметртэй тэгш бус байдал.14-15

Параметртэй экспоненциал тэгшитгэл ба тэгш бус байдал………16-17

Параметртэй логарифмын тэгшитгэл ба тэгш бус байдал......16-18

Улсын нэгдсэн шалгалтын зорилтууд……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………18-20 |

Бие даасан ажлын даалгавар …………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………21-28 |

Оршил.

Параметр бүхий тэгшитгэл ба тэгш бус байдал.

Хэрэв тэгшитгэл эсвэл тэгш бус байдалд зарим коэффициентийг тодорхой тоон утгыг өгөөгүй боловч үсгээр тэмдэглэсэн бол тэдгээрийг гэж нэрлэдэг. параметрүүд,тэгшитгэл буюу тэгш бус байдал нь өөрөө параметрийн.

Параметр бүхий тэгшитгэл эсвэл тэгш бус байдлыг шийдэхийн тулд та дараахь зүйлийг хийх хэрэгтэй.

Сонго онцгой утга- энэ нь тэгшитгэл эсвэл тэгш бус байдлын шийдэл өөрчлөгдөх эсвэл өнгөрөх үед параметрийн утга юм.

Тодорхойлох хүчинтэй утгууд- эдгээр нь тэгшитгэл эсвэл тэгш бус байдлын утга учиртай параметрийн утгууд юм.

Параметр бүхий тэгшитгэл эсвэл тэгш бус байдлыг шийдвэрлэх нь:

1) ямар параметрийн утгын шийдэл байгааг тодорхойлох;

2) параметрийн утгын зөвшөөрөгдөх систем бүрийн хувьд тохирох шийдлийн багцыг олно.

Та дараах аргуудыг ашиглан параметр бүхий тэгшитгэлийг шийдэж болно: аналитик эсвэл график.

Аналитик арга Энэ нь хэд хэдэн тохиолдлыг авч үзэх замаар тэгшитгэлийг судлах ажлыг багтаадаг бөгөөд тэдгээрийн аль нь ч алга.

Төрөл бүрийн параметр бүхий тэгшитгэл, тэгш бус байдлыг аналитик аргаар шийдвэрлэх нь нөхцөл байдлын нарийвчилсан дүн шинжилгээ хийх, тууштай судалгаа хийх шаардлагатай байдаг. "болгоомжтой харьцах"параметртэй.

График арга Энэ нь тэгшитгэлийн графикийг байгуулахад хамаарах бөгөөд үүнээс параметрийн өөрчлөлт нь тэгшитгэлийн шийдэлд хэрхэн нөлөөлж байгааг тодорхойлох боломжтой. График нь заримдаа асуудлыг шийдвэрлэхэд шаардлагатай, хангалттай нөхцлийг аналитик байдлаар томъёолох боломжийг олгодог. График шийдлийн арга нь тэгшитгэл нь параметрээс хамаарч хэдэн үндэстэй болохыг тогтоох шаардлагатай үед үр дүнтэй бөгөөд үүнийг тодорхой харах нь эргэлзээгүй давуу талтай юм.

§ 1. Шугаман тэгшитгэл ба тэгш бус байдал.

Шугаман тэгшитгэл А x = б , ерөнхий хэлбэрээр бичсэнийг параметртэй тэгшитгэл гэж үзэж болно, энд x - үл мэдэгдэх , а , б - сонголтууд. Энэ тэгшитгэлийн хувьд параметрийн тусгай буюу хяналтын утга нь үл мэдэгдэхийн коэффициент тэг болох утга юм.

Параметр бүхий шугаман тэгшитгэлийг шийдвэрлэхдээ параметр нь түүний тусгай утгатай тэнцүү, түүнээс ялгаатай тохиолдолд авч үздэг.

Тусгай параметрийн утга а үнэ цэнэ юм А = 0.

б = 0 нь тусгай параметрийн утга юм б .

At б ¹ 0 тэгшитгэлд шийдэл байхгүй.

At б = 0 тэгшитгэл нь дараах хэлбэртэй болно. 0x = 0. Энэ тэгшитгэлийн шийдэл нь дурын бодит тоо юм.

Маягтын тэгш бус байдал аа > б Тэгээд сүх < б (a ≠ 0)шугаман тэгш бус байдал гэж нэрлэдэг. Тэгш бус байдлын шийдлүүдийн багц аа >б- интервал

(; +), Хэрэв а > 0 , Мөн (-;) , Хэрэв А< 0 . Үүнтэй адил тэгш бус байдлын хувьд

Өө< б шийдлийн багц - интервал(-;), Хэрэв а > 0, Тэгээд (; +), Хэрэв А< 0.

Жишээ 1. Тэгшитгэлийг шийд сүх = 5

Шийдэл: Энэ бол шугаман тэгшитгэл юм.

Хэрэв a = 0, дараа нь тэгшитгэл 0 × x = 5шийдэл байхгүй.

Хэрэв А¹ 0, x =- тэгшитгэлийн шийдэл.

Хариулах: цагт А¹ 0, x=

a = 0-ийн хувьд шийдэл байхгүй.

Жишээ 2. Тэгшитгэлийг шийд сүх – 6 = 2а – 3х.

Шийдэл:Энэ бол шугаман тэгшитгэл, сүх – 6 = 2а – 3х (1)

сүх + 3х = 2а +6

Тэгшитгэлийг дахин бичих (a+3)x = 2(a+3), хоёр тохиолдлыг авч үзье:

a= -3Тэгээд А¹ -3.

Хэрэв a= -3, дараа нь дурын бодит тоо X(1) тэгшитгэлийн язгуур юм. Хэрэв А¹ -3 , тэгшитгэл (1) нь нэг үндэстэй x = 2.

Хариулт: At a = -3, x Р ; цагт А ¹ -3, x = 2.

Жишээ 3. Ямар параметрийн утгууд дээр Атэгшитгэлийн язгууруудын дунд

2 цаг – 4 цаг – а 2 + 4a – 4 = 0илүү олон үндэс бий 1 ?

Шийдэл: Тэгшитгэлээ шийдье 2 цаг – 4 цаг – а 2 + 4a – 4 = 0- шугаман тэгшитгэл

2(a - 2) x = a 2 – 4a +4

2(a - 2) x = (a - 2) 2

At a = 2тэгшитгэлийг шийдвэрлэх 0x = 0 1-ээс ихийг оруулаад дурын тоо байх болно.

At А¹ 2 x =
. Нөхцөлөөр x > 1, тэр бол
>1 ба >4.

Хариулт: At А (2) U (4;∞).

Жишээ 4 . Параметрийн утга бүрийн хувьд Атэгшитгэлийн язгуурын тоог ол аа=8.

Шийдэл. сүх = 8- шугаман тэгшитгэл.

y = а- хэвтээ шугамын гэр бүл;

y = - График нь гипербол юм. Эдгээр функцүүдийн графикийг бүтээцгээе.

Хариулт: Хэрэв a =0, тэгвэл тэгшитгэлд шийдэл байхгүй болно. Хэрэв a ≠ 0, тэгвэл тэгшитгэл нь нэг шийдэлтэй байна.

Жишээ 5 . График ашиглан тэгшитгэл хэдэн үндэстэй болохыг олж мэд.

|x| = аа - 1.

у =| x | ,

y = аа - 1– График нь цэгийг дайран өнгөрөх шулуун шугам юм (0;-1).

Эдгээр функцүүдийн графикийг бүтээцгээе.

Хариулт: Хэзээ |a|>1- нэг үндэс

цагт | a|≤1 - тэгшитгэл нь үндэсгүй.

Жишээ 6 . Тэгш бус байдлыг шийдэх сүх + 4 > 2х + a 2

Шийдэл : сүх + 4 > 2х + a 2
(a – 2) x >А 2 – 4. Гурван тохиолдлыг авч үзье.

Хариулт. x > a + 2цагт a > 2; X<а + 2, цагт А< 2; цагт a=2шийдэл байхгүй.

§ 2. Квадрат тэгшитгэл ба тэгш бус байдал

Квадрат тэгшитгэлхэлбэрийн тэгшитгэл юм Өө ² + б x + c = 0 , Хаана a≠ 0,

А, б , Хамт - сонголтууд.

Параметр бүхий квадрат тэгшитгэлийг шийдэхийн тулд та дараах томъёог ашиглан стандарт шийдлийн аргыг ашиглаж болно.

1 ) квадрат тэгшитгэлийн дискриминант: Д = б ² - 4 ac , (
²- ac)

2) Квадрат тэгшитгэлийн язгуурын томъёо:X 1 =
, X 2 =
,

(X 1,2 =
)

Квадрат тэгш бус байдал гэж нэрлэдэг

а X 2 + б x + c > 0,а X 2 + б x + в< 0, (1), (2)

а X 2 + б x + c ≥ 0,а X 2 + б x + c ≤ 0,(3), (4)

Тэгшитгэлгүй байдлын шийдийн багц (3) нь тэгш бус байдлын шийдэл (1) ба тэгшитгэлийн багцыг нэгтгэснээр олддог. , а X 2 + б x + c = 0.Тэгш бус байдлын шийдлүүдийн багцыг (4) ижил төстэй байдлаар олж болно.

Хэрэв квадрат гурвалжны дискриминант а X 2 + б x + в тэгээс бага бол a > 0-ийн хувьд гурвалсан тоо нь бүх х-д эерэг байна Р.

Хэрэв квадрат гурвалжин үндэстэй бол (x 1 < х 2 ), тэгвэл a > 0 бол олонлог дээр эерэг байна(-; x 2 )
(X 2; +) интервал дээр сөрөг байна

(x 1; x 2 ). Хэрвээ< 0, то трехчлен положителен на интервале (х 1 ; x 2 ) ба бүх x-д сөрөг (-; x 1 )
(X 2; +).

Жишээ 1. Тэгшитгэлийг шийд ax² - 2 (a – 1)x – 4 = 0.

Энэ бол квадрат тэгшитгэл юм

Шийдэл: Тусгай утга a = 0.

At a = 0Бид шугаман тэгшитгэлийг авна 2х – 4 = 0. Энэ нь нэг үндэстэй x = 2.

At a ≠ 0.Ялгаварлагчийг олцгооё.

Д = (a-1)² + 4a = (a+1)²

Хэрэв a = -1,Тэр Д = 0 - нэг үндэс.

Орлуулж үндсийг нь олъё a = -1.

-x² + 4x – 4= 0,тэр бол x² -4x + 4 = 0,бид үүнийг олдог x=2.

Хэрэв a ≠ - 1, Тэр Д >0 . Үндэс томъёог ашиглан бид дараахь зүйлийг авна.x=
;

X 1 =2, x 2 = -.

Хариулт: At a=0 ба a= -1тэгшитгэл нь нэг үндэстэй x = 2;цагт a ≠ 0 ба

А ≠ - 1 тэгшитгэл нь хоёр үндэстэйX 1 =2, x 2 =-.

Жишээ 2. Энэ тэгшитгэлийн язгуурын тоог ол x²-2x-8-a=0параметрийн утгаас хамаарна А.

Шийдэл. Энэ тэгшитгэлийг хэлбэрээр дахин бичье x²-2x-8=a

y = x²-2x-8- график нь парабол;

y =а- хэвтээ шугамын гэр бүл.

Функцийн графикуудыг байгуулъя.

Хариулт: Хэзээ А<-9 , тэгшитгэлд шийдэл байхгүй; a=-9 үед тэгшитгэл нэг шийдтэй байна; цагт a>-9, тэгшитгэл нь хоёр шийдэлтэй.

Жишээ 3. Юун дээр Атэгш бус байдал (a – 3) x 2 – 2ax + 3a – 6 >0 x-ийн бүх утгуудад тохирох уу?

Шийдэл.Квадрат гурвалсан тоо нь x if-ийн бүх утгуудад эерэг байна

a-3 > 0 ба Д<0, т.е. при а, удовлетворяющих системе неравенств

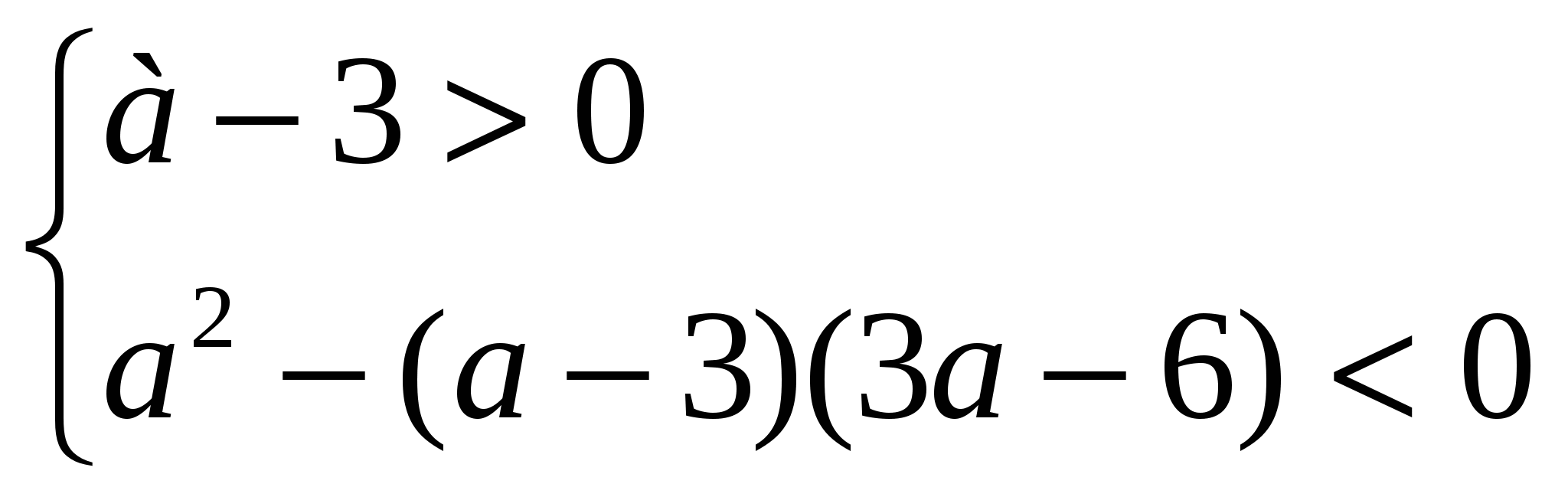
, үүнээс үүдэн үүнийг дагадага > 6 .

Хариулт.а > 6

§ 3. Параметртэй бутархай рационал тэгшитгэл,

шугаман болгон бууруулж болно

Бутархай тэгшитгэлийг шийдвэрлэх үйл явц нь ердийн схемийн дагуу явагддаг: тэгшитгэлийн хоёр талыг зүүн ба баруун талуудын нийтлэг хуваагчаар үржүүлэх замаар бутархайг бүхэл тоогоор солино. Үүний дараа гаднах үндэс, өөрөөр хэлбэл хуваагчийг тэг болгож хувиргах тоонуудыг оруулалгүйгээр тэгшитгэлийг бүхэлд нь шийднэ.

Параметр бүхий тэгшитгэлийн хувьд энэ асуудал илүү төвөгтэй байдаг. Энд гаднах үндсийг "арилгах" тулд нийтлэг хуваагчийг тэг болгон хувиргах параметрийн утгыг олох, өөрөөр хэлбэл параметрийн харгалзах тэгшитгэлийг шийдэх шаардлагатай.

Жишээ 1. Тэгшитгэлийг шийд
= 0

Шийдэл: D.Z: x +2 ≠ 0, x ≠ -2

x – a = 0, x = a.

Хариулт: At a ≠ - 2, x=a

At a = -2үндэс байхгүй.

Жишээ 2 . Тэгшитгэлийг шийд
-
=
(1)

Энэ бол бутархай рационал тэгшитгэл юм

Шийдэл:Утга a = 0онцгой юм. At a = 0тэгшитгэл нь ямар ч утгагүй тул үндэсгүй. Хэрэв a ≠ 0,Дараа нь хувиргасны дараа тэгшитгэл нь дараах хэлбэртэй болно. x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- квадрат тэгшитгэл.

Ялгаварлагчийг олцгооё = (1 – a)² - (a² - 2a – 3)= 4, тэгшитгэлийн язгуурыг олX 1 = a + 1, x 2 = a - 3.

(1) тэгшитгэлээс (2) тэгшитгэл рүү шилжих үед (1) тэгшитгэлийн тодорхойлолтын хүрээ өргөжиж, энэ нь гадны үндэс гарч ирэхэд хүргэж болзошгүй юм. Тиймээс баталгаажуулах шаардлагатай.

Шалгалт.Олдсон утгуудаас хасъя Xбайгаа хүмүүс

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Хэрэв X 1 +1=0, тэр бол (a+1) + 1= 0, Тэр a= -2.Тиймээс,

цагт a= -2 , X 1 -

Хэрэв X 1 +2=0, тэр бол (a+1)+2=0,Тэр a = - 3. Тиймээс, хэзээ a = - 3, x 1 - тэгшитгэлийн гадаад үндэс. (1).

Хэрэв X 2 +1=0, тэр бол (a – 3) + 1= 0, Тэр a = 2. Тиймээс, хэзээ a = 2 x 2 - тэгшитгэлийн гадаад үндэс (1).

Хэрэв X 2 +2=0, тэр бол ( a – 3) + 2 = 0,Тэр a=1. Тиймээс, хэзээ a = 1,

X 2 - тэгшитгэлийн гадаад үндэс (1).

Үүний дагуу хэзээ a = - 3бид авдаг x = - 3 – 3 = -6;

цагт a = - 2 x = -2 – 3= - 5;

цагт a = 1 x =1 + 1= 2;

цагт a = 2 x = 2+1 = 3.

Та хариултаа бичиж болно.

Хариулт: 1) хэрэв a= -3,Тэр x= -6; 2) хэрэв a= -2, Тэр x= -5; 3) хэрэв a= 0, тэгвэл үндэс байхгүй; 4) хэрэв a= 1, Тэр x=2; 5) хэрэв a=2, Тэр x=3; 6) хэрэв a ≠ -3, a ≠ -2, a ≠ 0, a≠ 1, a ≠ 2, дараа нь x 1 = a + 1, x 2 = a-3.

§4. Иррационал тэгшитгэл ба тэгш бус байдал

Үндэс тэмдгийн дор хувьсагч агуулагдсан тэгшитгэл ба тэгш бус байдлыг нэрлэнэ үндэслэлгүй.

Иррационал тэгшитгэлийг шийдэх нь тэгшитгэлийн хоёр талыг экспоненциаллах эсвэл хувьсагчийг орлуулах замаар иррациональ тэгшитгэлээс рационал тэгшитгэл рүү шилжих явдал юм. Тэгшитгэлийн хоёр талыг тэгш түвшинд өсгөхөд гадны үндэс гарч ирж болно. Тиймээс, энэ аргыг ашиглахдаа параметрийн утгын өөрчлөлтийг харгалзан олсон бүх үндсийг анхны тэгшитгэлд орлуулах замаар шалгах хэрэгтэй.

Маягтын тэгшитгэл
=g (x) нь системтэй тэнцүү байна

f (x) ≥ 0 тэгш бус байдал нь f (x) = g 2 (x) тэгшитгэлээс үүснэ.

Иррационал тэгш бус байдлыг шийдвэрлэхдээ бид дараах эквивалент хувиргуудыг ашиглана.

≤ g(x)


≥g(x)

Жишээ 1. Тэгшитгэлийг шийд
= x + 1 (3)

Энэ бол иррациональ тэгшитгэл юм

Шийдэл: Арифметик язгуурын тодорхойлолтоор (3) тэгшитгэл нь системтэй тэнцүү байна
.

At a = 2системийн эхний тэгшитгэл нь хэлбэртэй байна 0 x = 5, өөрөөр хэлбэл ямар ч шийдэлгүй.

At a≠ 2 x=
. Ямар үнэ цэнийн талаар олж мэдьеА үнэ цэнийг олсонX тэгш бус байдлыг ханганаx ≥ -1:
≥ - 1,
≥ 0,

хаана a ≤эсвэл a > 2.

Хариулт: At a≤, a > 2 x=
, цагт < а ≤ 2 тэгшитгэлд шийдэл байхгүй.

Жишээ 2. Тэгшитгэлийг шийд
= a (Хавсралт 4)

Шийдэл. y =

y = a– хэвтээ шугамын гэр бүл.

Функцийн графикуудыг байгуулъя.

Хариулах: цагт А<0 - шийдэл байхгүй;

цагт А≥ 0 - нэг шийдэл.

Жишээ 3 . Тэгш бус байдлыг шийдье(a+1)
<1.

Шийдэл.О.Д.З. x ≤ 2. Хэрэв a+1 ≤0, дараа нь тэгш бус байдал нь бүх зөвшөөрөгдөх утгуудад тохирно X. Хэрэв a+1>0, Тэр

(a+1)
<1.

<

хаана X (2-
2

Хариулт. X (- ;2a (-;-1, X (2-
2

цагт А (-1;+).

§ 5. Тригонометрийн тэгшитгэл ба тэгш бус байдал.

Хамгийн энгийн тригонометрийн тэгшитгэлийг шийдэх томьёо энд байна.

Синкс = a
x= (-1) n arcsin a+πn, n З, ≤1, (1)

Cos x = a
x = ±arccos a + 2 πn, n З, ≤1. (2)

Хэрэв >1, тэгвэл (1) ба (2) тэгшитгэлд шийдэл байхгүй болно.

tan x = a
x= arctan a + πn, n З,а Р

ctg x = a
x = arcctg a + πn, n З,а Р

Стандарт тэгш бус байдал бүрийн хувьд бид шийдлүүдийн багцыг заана.

1. sin x > a
arcsin a + 2 πn З,

цагт а <-1, x Р ; цагт а ≥ 1, шийдэл байхгүй.

2. . гэм х< a
π - arcsin a + 2 πnZ,

a≤-1-ийн хувьд шийдэл байхгүй; > 1-ийн хувьд,x Р

3. cos x > а
- arccos а + 2 πn < x < arccos а + 2 πn , n З ,

цагт А<-1, x Р ; цагт а ≥ 1 , шийдэл байхгүй.

4. cos x arccos a+ 2 πnZ,

цагт a≤-1 , шийдэл байхгүй; цагта > 1, x Р

5. tan x > a, арктан a + πnZ

6.тг х< a, -π/2 + πn Z

Жишээ 1. Хай А, энэ тэгшитгэл нь шийдэлтэй байна:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Шийдэл.Тэгшитгэлийг хэлбэрээр бичье

-тайos 2 x + (2 а -4) cosx +(а – 5)(a+1) =0,Үүнийг квадрат хэлбэрээр шийдвэл бид олж авна cosx = 5-АТэгээд cosx = -a-1.

Тэгшитгэл cosx = 5- А өгөгдсөн шийдлүүд байна -1≤ 5-А ≤1
4≤ А≤ 6 ба тэгшитгэл. cosx = - a-1 өгсөн -1≤ -1-А ≤ 1
-2 ≤ А ≤0.

Хариулт. А -2; 0
4; 6

Жишээ 2. Юун дээр бтэгш бус байдал бий
+ б> 0 нь бүх x ≠-д тохирноπn , n З .

Шийдэл.тавья А= 0. b >0 үед тэгш бус байдал биелнэ. Одоо b ≤0 нь асуудлын нөхцөлийг хангахгүй гэдгийг харуулъя. Үнэхээр x = тавихад л хангалттай π /2, Хэрэв А <0, и х = - π /2 цагт А ≥0.

Хариулт.b>0

§ 6. Экспоненциал тэгшитгэл ба тэгш бус байдал

1. Тэгшитгэл h(x) е ( x ) = h(x) g ( x) цагт h(x) > 0 нь хоёр системийн цуглуулгатай тэнцэнэ
Тэгээд

2. Онцгой тохиолдолд (h (x)= а ) тэгшитгэл А f(x) = А g(x) цагт А> 0 нь хоёр системийн цуглуулгатай тэнцэнэ

Тэгээд

3. Тэгшитгэл А f(x) = б , Хаана А > 0, а ≠1, б>0, тэгшитгэлтэй тэнцүү

f (x )= log a b . Болж байна А=1-ийг тусад нь авч үзнэ.

Хамгийн энгийн экспоненциал тэгш бус байдлын шийдэл нь чадлын шинж чанарт суурилдаг. Маягтын тэгш бус байдале(а x ) > 0 хувьсагчийн өөрчлөлтийг ашигланат= а x тэгш бус байдлын системийг шийдвэрлэхэд хүргэдэг
дараа нь харгалзах энгийн экспоненциал тэгш бус байдлыг шийдвэрлэх.

Хатуу бус тэгш бус байдлыг шийдвэрлэхдээ хатуу тэгш бус байдлын шийдийн багцад харгалзах тэгшитгэлийн язгуурыг нэмэх шаардлагатай. Илэрхийлэл агуулсан бүх жишээн дэх тэгшитгэлийг шийдвэрлэхтэй адил А f (x) гэж бид таамаглаж байна А> 0. Тохиолдол А= 1-ийг тусад нь авч үзнэ.

Жишээ 1 . Юун дээр Атэгшитгэл 8 x =
зөвхөн эерэг үндэстэй юу?

Шийдэл. Нэгээс их суурьтай экспоненциал функцийн шинж чанараар бид x>0 байна
8 X >1

>1

>0, хаанааса (1,5;4).

Хариулт. а (1,5;4).

Жишээ 2. Тэгш бус байдлыг шийдэх а 2 ∙2 x > а

Шийдэл. Гурван тохиолдлыг авч үзье:

1. А< 0 . Тэгш бус байдлын зүүн тал эерэг, баруун тал нь сөрөг байх тул тэгш бус байдал нь дурын х-д тохирно Р.

2. а=0. Ямар ч шийдэл байхгүй.

3. А > 0 . а 2 ∙2 x > a
2 x >
x > -лог 2 а

Хариулт. X Рцагт А > 0; шийдэл байхгүй а =0; X (- бүртгэл 2 а; +) цагтa> 0 .

§ 7. Логарифмын тэгшитгэл ба тэгш бус байдал

Шийдвэрлэхдээ ашигласан зарим эквивалентуудыг танилцуулъя логарифмын тэгшитгэл ба тэгш бус байдал.

1. log f (x) g (x) = log f (x) h (x) тэгшитгэл нь системтэй тэнцүү байна.

Ялангуяа, хэрэв А >0, А≠1, тэгвэл

бүртгэл а g(x)=лог а h(x)

2. Тэгшитгэл бүртгэл а g(x)=b
g(x)=а б ( А >0, a ≠ 1, g(x) >0).

3. Тэгш бус байдал бүртгэл е ( x ) g (x) ≤ бүртгэл е ( x ) h(x) нь хоёр системийн хослолтой тэнцүү байна:
Тэгээд

Хэрвээ, b нь тоо, a >0, a ≠1, тэгвэл

бүртгэл а f(x) ≤ b

бүртгэл а f(x)>b

Жишээ 1. Тэгшитгэлийг шийд

Шийдэл. ODZ-ийг олъё: x > 0, x ≠ А 4 , а > 0, А≠ 1. Тэгшитгэлийг хувирга

бүртгэл x – 2 = 4 – бүртгэл а x
бүртгэл x + бүртгэл а x– 6 = 0, хаанаас бүртгэл а x = - 3

x = А-3 ба бүртгэл а x = 2
x = А 2. Нөхцөл x = А 4
А – 3 = А 4 эсвэл А 2 = А 4 ODZ дээр хийгддэггүй.

Хариулт: x = А-3, x = А 2 цагт А (0; 1)
(1; ).

Жишээ 2 . Хамгийн их утгыг ол А, үүний төлөө тэгшитгэл

2 бүртгэл -
+ а = 0 шийдэлтэй.

Шийдэл. Бид солих болно
= тБид 2-р квадрат тэгшитгэлийг авнат 2 – т + а = 0. Шийдвэрлэхдээ бид олноД = 1-8 а . Ингээд авч үзье Д≥0, 1-8 А ≥0
А ≤.

At А = квадрат тэгшитгэл нь үндэстэйт= >0.

Хариулт. А =

Жишээ 3 . Тэгш бус байдлыг шийдэхбүртгэл(x 2 – 2 x + а ) > - 3

Шийдэл. Тэгш бус байдлын системийг шийдье

Квадрат гурвалсан тоонуудын үндэс x 1,2 = 1 ±
тэдний 3,4 = 1 ±
.

Чухал параметрийн утга: А= 1 ба А= 9.

X 1 ба X 2 нь эхний ба хоёр дахь тэгш бус байдлын шийдүүдийн багц байцгаая

X 1
X 2 = X – анхны тэгш бус байдлын шийдэл.

0-д< а <1 Х 1 = (- ;1 -
)
(1 +
; +), цагтА> 1 X 1 = (-;+).

0-д< а < 9 Х 2 = (1 -
; 1 +
), цагтА≥9 X 2 – шийдэл байхгүй.

Гурван тохиолдлыг авч үзье:

1. 0< а ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < а < 9 Х = (1 -
;1 +
).

3. а≥ 9 X – шийдэл байхгүй.

Улсын нэгдсэн шалгалтын зорилго

Өндөр түвшний C1, C2

Жишээ 1. Бүх утгыг ол Р, үүний төлөө тэгшитгэл

Р ∙ ctg 2x+2sinx+ х= 3 нь дор хаяж нэг үндэстэй.

Шийдэл.Тэгшитгэлийг өөрчилье

Р ∙ (
- 1) + 2sinx + х= 3, sinx =t, т
,т 0.

- х+2т+ х = 3, + 2 т = 3, 3 -2т = , 3т 2 – 2т 3 = х .

Болъё е(y) = 3 т 2 – 2 т 3 . Функцийн утгуудын багцыг олъёе(x) дээр


. цагт / = 6 т – 6 т 2 , 6 т - 6 т 2 = 0, т 1 =0, т 2 = 1. е(-1) = 5, е(1) = 1.

At т
, Э(е) =
,

At т
, Э(е) =
, өөрөөр хэлбэл хэзээ т


, Э(е) =
.

3-р тэгшитгэл рүүт 2 – 2 т 3 = х (тиймээс өгөгдсөн) дор хаяж нэг үндэс шаардлагатай, хангалттай байсанх Э(е), тэр бол х
.

Хариулт.
.

Жишээ 2.

Ямар параметрийн утгууд дээрАтэгшитгэл бүртгэл
(4 x 2 – 4 а + а 2 +7) = 2 яг нэг үндэстэй юу?

Шийдэл.Тэгшитгэлийг үүнтэй ижил тэнцүү болгон хувиргацгаая.

4x 2 – 4 а + а 2 +7 = (x 2 + 2) 2.

Хэрэв тодорхой x тоо нь үүссэн тэгшитгэлийн үндэс бол - x тоо нь мөн энэ тэгшитгэлийн үндэс болохыг анхаарна уу. Нөхцөлөөр бол энэ нь боломжгүй тул цорын ганц үндэс нь 0 тоо юм.

Бид олох болно А.

4∙ 0 2 - 4а + а 2 +7 = (0 2 + 2) 2 ,

а 2 - 4а +7 = 4, а 2 - 4а +3 = 0, а 1 = 1, а 2 = 3.

Шалгалт.

1) а 1 = 1. Дараа нь тэгшитгэл нь дараах байдалтай байна.бүртгэл
(4 x 2 +4) =2. Үүнийг шийдье

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 нь цорын ганц үндэс юм.

2) а 2 = 3. Тэгшитгэл нь дараах байдалтай байна.бүртгэл
(4 x 2 +4) =2
x = 0 нь цорын ганц үндэс юм.

Хариулт. 1; 3

Өндөр түвшний C4, C5

Жишээ 3. Бүх утгыг ол R,Үүний тэгшитгэл

x 2 – ( Р+ 3)x + 1= 0 нь бүхэл язгууртай ба эдгээр язгуурууд нь тэгш бус байдлын шийдэл юм: x 3 – 7 Р x 2 + 2x 2 – 14 Р x - 3x +21 Р ≤ 0.

Шийдэл. x байг 1, X 2 – x тэгшитгэлийн бүхэл язгуурууд 2 – (Р + 3)x + 1= 0. Дараа нь Вьетагийн томъёоны дагуу x тэнцүү байна 1 + x 2 = Р + 3, x 1 ∙ x 2 = 1. Хоёр бүхэл тооны үржвэр х 1 , X 2 Зөвхөн хоёр тохиолдолд нэгтэй тэнцүү байж болно: x 1 = x 2 = 1 эсвэл x 1 = x 2 = - 1. Хэрэв x бол 1 = x 2 = 1, тэгвэлР + 3 = 1+1 = 2
Р = - 1; хэрэв x 1 = x 2 = - 1, тэгвэлР + 3 = - 1 – 1 = - 2
Р = - 5. Тэгшитгэлийн язгуурууд x эсэхийг шалгая 2 – (Р + 3)x + 1= 0 нь энэ тэгш бус байдлын шийдлээр тайлбарласан тохиолдолд. Энэ үйл явдалд зориулжР = - 1, x 1 = x 2 = 1 бидэнд байна

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – үнэн; тохиолдуулан Р= - 5, x 1 = x 2 = - 1 бидэнд (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – зөв. Тиймээс асуудлын нөхцөл нь зөвхөн хангагдана Р= - 1 ба Р = - 5.

Хариулт.Р 1 = - 1 ба Р 2 = - 5.

Жишээ 4. Параметрийн бүх эерэг утгыг ол А, түүний хувьд 1-ийн тоо нь функцийн тодорхойлолтын мужид хамаарна

цагт = (А
- А
).

Курсын ажил

Гүйцэтгэгч: Бугров С.К.

Олон физик процесс, геометрийн хэв маягийг судлах нь ихэвчлэн параметртэй асуудлыг шийдвэрлэхэд хүргэдэг. Зарим их дээд сургуулиуд шалгалтын хуудсанд тэгшитгэл, тэгш бус байдал, тэдгээрийн системийг оруулдаг бөгөөд энэ нь ихэвчлэн маш төвөгтэй бөгөөд шийдвэрлэхэд стандарт бус хандлагыг шаарддаг. Сургуулийн хувьд энэ нь сургуулийн математикийн хичээлийн хамгийн хэцүү хэсгүүдийн нэгийг зөвхөн сонгон суралцах цөөн хэдэн ангид л авч үздэг.

Энэ ажлыг бэлтгэхдээ би энэ сэдвийг илүү гүнзгий судалж, хариултанд хурдан хүргэх хамгийн оновчтой шийдлийг тодорхойлох зорилго тавьсан. Миний бодлоор график арга нь параметр бүхий тэгшитгэл, тэгш бус байдлыг шийдвэрлэх хялбар бөгөөд хурдан арга юм.

Миний эссэ нь тэгшитгэлийн төрөл, тэгш бус байдал, тэдгээрийн тогтолцооны талаар ярилцдаг бөгөөд ажлын явцад олж авсан мэдлэг маань сургуулийн шалгалт өгөх, их сургуульд ороход надад тусална гэж найдаж байна.

§ 1. Үндсэн тодорхойлолтууд

Тэгшитгэлийг авч үзье

¦(a, b, c, …, k, x)=j(a, b, c, …, k, x), (1)

Үүнд: a, b, c, …, k, x нь хувьсах хэмжигдэхүүн юм.

Аливаа хувьсах утгын систем

a = a0, b = b0, c = c0, …, k = k0, x = x0,

Энэ тэгшитгэлийн зүүн ба баруун тал хоёулаа бодит утгыг авдаг бол a, b, c, ..., k, x хувьсагчдын зөвшөөрөгдөх утгуудын систем гэж нэрлэдэг. A нь a-ийн бүх зөвшөөрөгдөх утгуудын багц, B нь b гэх мэт бүх зөвшөөрөгдөх утгуудын олонлог, X нь x-ийн бүх зөвшөөрөгдөх утгуудын олонлог, өөрөөр хэлбэл. аОА, bОB, …, xОX. Хэрэв A, B, C, …, K олонлог бүрд a, b, c, …, k утгыг тус тус сонгон засаад (1) тэгшитгэлд орлуулж байвал x-ийн тэгшитгэлийг олж авна. өөрөөр хэлбэл нэг үл мэдэгдэх тэгшитгэл.

Тэгшитгэлийг шийдвэрлэхэд тогтмол гэж тооцогддог a, b, c, ..., k хувьсагчдыг параметр, тэгшитгэлийг өөрөө параметр агуулсан тэгшитгэл гэнэ.

Параметрүүдийг латин цагаан толгойн эхний үсгээр тэмдэглэнэ: a, b, c, d, ..., k, l, m, n, үл мэдэгдэхийг x, y, z үсгээр тэмдэглэнэ.

Параметр бүхий тэгшитгэлийг шийдэх гэдэг нь параметрийн ямар утгуудад шийдэл байгаа, тэдгээр нь юу болохыг харуулах гэсэн үг юм.

Дараах тохиолдолд ижил параметрүүдийг агуулсан хоёр тэгшитгэлийг эквивалент гэж нэрлэдэг.

a) тэдгээр нь ижил параметрийн утгын хувьд утга учиртай;

б) эхний тэгшитгэлийн шийдэл бүр хоёр дахь тэгшитгэлийн шийдэл ба эсрэгээр.

§ 2. Шийдлийн алгоритм.

Тэгшитгэлийн тодорхойлолтын мужийг ол.

Бид a-г х-ийн функцээр илэрхийлнэ.

XOa координатын системд бид энэ тэгшитгэлийн тодорхойлолтод багтсан x-ийн утгуудын хувьд a=¦(x) функцийн графикийг байгуулна.

cÎ(-¥;+¥) функцийн графиктай a=c шулууны огтлолцох цэгүүдийг олно.Хэрэв a=c шулуун нь a=¦(x) графикийг огтолж байвал. , дараа нь бид огтлолцох цэгүүдийн абсциссыг тодорхойлно. Үүний тулд x-ийн хувьд a=¦(x) тэгшитгэлийг шийдэхэд хангалттай.

Бид хариултаа бичнэ.

I. Тэгшитгэлийг шийд

(1)

x=0 нь тэгшитгэлийн үндэс биш тул тэгшитгэлийг дараах байдлаар шийдэж болно.

эсвэл

Функцийн график нь хоёр "наасан" гипербол юм. Анхны тэгшитгэлийн шийдийн тоог баригдсан шугам ба шулуун шугамын огтлолцох цэгүүдийн тоогоор тодорхойлно y=a.

Хэрэв a О (-¥;-1]П(1;+¥)П

, тэгвэл y=a шулуун нь (1) тэгшитгэлийн графикийг нэг цэгт огтолно. Бид x-ийн тэгшитгэлийг шийдэхдээ энэ цэгийн абсциссыг олох болно.

Тиймээс энэ интервал дээр тэгшитгэл (1) шийдэлтэй байна

. , тэгвэл y=a шулуун нь (1) тэгшитгэлийн графикийг хоёр цэгээр огтолно. Эдгээр цэгүүдийн абсциссуудыг ба тэгшитгэлээс олж болно, бид ба . , тэгвэл y=a шулуун нь (1) тэгшитгэлийн графиктай огтлолцохгүй тул шийдэл байхгүй.

Хэрэв a О (-¥;-1]П(1;+¥)П

, Тэр ; , Тэр , ; , тэгвэл ямар ч шийдэл байхгүй.

II. Тэгшитгэл болох a параметрийн бүх утгыг ол

гурван өөр үндэстэй.

Тэгшитгэлийг дахин бичих

хос функцийг судалж үзээд та а параметрийн хүссэн утгууд нь функцийн графиктай огтлолцох яг гурван цэгтэй функцийн графикийн байрлалтай тохирч байгааг анзаарч болно. .

xOy координатын системд бид функцийн графикийг байгуулна

). Үүнийг хийхийн тулд бид үүнийг хэлбэрээр илэрхийлж болох бөгөөд үүссэн дөрвөн тохиолдлыг авч үзээд бид энэ функцийг хэлбэрээр бичнэ.

Функцийн графикаас хойш

- энэ нь Ox тэнхлэгтэй тэнцүү налуу өнцөгтэй шулуун шугам бөгөөд Oy тэнхлэгийг координаттай (0, a) цэгээр огтолж байгаа тул заасан гурван огтлолцлын цэгийг зөвхөн дараах тохиолдолд олж авах боломжтой гэж бид дүгнэж байна. Энэ шугам нь функцийн графикт хүрнэ. Тиймээс бид деривативыг олдог.

III. a параметрийн бүх утгыг олоорой, тус бүрийн хувьд тэгшитгэлийн систем байна

шийдэлтэй.

Системийн эхний тэгшитгэлээс бид олж авна

Тиймээс, энэ тэгшитгэл нь "хагас параболын" бүлгийг тодорхойлдог - параболын баруун мөчрүүд нь абсцисса тэнхлэгийн дагуу оройтой "гулсдаг".

Хоёр дахь тэгшитгэлийн зүүн талд байгаа бүтэн квадратуудыг сонгоод үржвэр болгоё

Онгоцны олон цэгүүд

Хоёр дахь тэгшитгэлийг хангах нь хоёр шулуун ба

"Семипарабол"-ын гэр бүлийн муруй параметрийн ямар утгуудад үүссэн шулуун шугамын аль нэгтэй дор хаяж нэг нийтлэг цэг байгааг олж мэдье.

"Параметртэй асуудлыг шийдэж сурах" цуврал

IV. Параметртэй квадрат тэгшитгэл ба тэгш бус байдал

IV.1. Үндсэн ойлголтууд

Тодорхойлолт. (1) хэлбэрийн функц, энд , , нь параметрийн өгөгдсөн функцууд юм А, тэдгээрийн тодорхойлолтын мужуудын огтлолцол дээр авч үзэх нь параметртэй квадрат функц гэж нэрлэгдэх болно А.

Жишээ.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Тодорхойлолт. Параметртэй (1) квадрат функцийн тодорхойлолтын дэд домайн АБид хос утгуудын багцыг бүхэлд нь ойлгох болно XТэгээд Атөрөл ( X; А), тус бүрийн хувьд илэрхийлэл утгаа алддаггүй.

1-10-р функцүүдийн тодорхойлолтын мужуудыг тогтооцгооё.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Хэрэв параметр нь -аас тоон утгуудын аль нэгийг авбал (1) функц нь тоон коэффициент бүхий функцүүдийн аль нэг хэлбэрийг авна.

; ; ;
; ; ; ,

Хаана к, б, в- бодит тоо.

Параметрийн зарим утгуудын хувьд параметр бүхий квадрат функц нь параметргүй квадрат функц эсвэл шугаман хэлбэртэй байдаг гэдгийг анхаарна уу.

Параметр бүхий квадрат функц нь ихэвчлэн тоон коэффициент бүхий квадрат эсвэл шугаман функцүүдийн бүлгийг "үүсгэдэг" тул параметртэй квадрат функцийн графикууд, бид энэ гэр бүлийн олон графикийг хэлэх болно.

Тодорхойлолт. А-ийг (1) хэлбэрийн тэгшитгэл гэж нэрлэдэг бөгөөд , , параметрийн эдгээр функцууд юм А, тэдгээрийн тодорхойлолтын хүрээнүүдийн огтлолцол дээр авч үздэг.

Ялангуяа зарим коэффициент эсвэл таслах нэр томъёо нь тоо байж болно.

Жишээ.

, (1)
, (2)
, (3)
, (4)
. (5)

Параметртэй квадрат функцийн тодорхойлолтыг ашиглан бид параметртэй квадрат тэгшитгэлийн дараах тодорхойлолтыг өгч болно.

Тодорхойлолт. Параметртэй квадрат тэгшитгэл Ахэлбэрийн тэгшитгэл гэж нэрлэгддэг ба энд параметртэй квадрат функц байна А.

Хэрэв бол (1) тэгшитгэл нь уламжлалт утгаараа квадрат, өөрөөр хэлбэл. хоёрдугаар зэрэг.
Хэрэв бол (1) тэгшитгэл шугаман болно.

Бүх хүчинтэй параметрийн утгуудын хувьд А, үүний төлөө ба , мэдэгдэж буй томьёо ашиглан бид (1) тэгшитгэлийн язгуурыг параметрийн хувьд илэрхийлдэг.

Эдгээр үнэт зүйлс А, үүнд , онцгой тохиолдол гэж тусад нь авч үзэх ёстой.
Жишээлбэл, (5) тэгшитгэл нь , эндээс хэлбэртэй байна.

IV.2. Параметр бүхий квадрат тэгшитгэл

№1. Тэгшитгэлийг шийд.

– тэгшитгэл-үр дагавар. Бид авна: , .

Координатын системд ( өө) бид шийдлийг дуусгана. (Зураг 1)

Хариулт: 1. Хэрэв , тэгвэл .

2. Хэрэв , тэгвэл .

3. Хэрэв , , тэгвэл , .

№2. Параметрийн утгыг ол А, тэгшитгэл нь нэг язгууртай. Хэрэв хэд хэдэн ийм утгууд байгаа бол тэдгээрийн нийлбэрийг хариултдаа бичнэ үү.

Энэ тэгшитгэл нь ижил төстэй систем болгон бууруулна:

Үүнийг хэлбэрт оруулаад координатын системд графикаар шийдье ( xOa). (Зураг 2).

Тэгшитгэл нь нэг язгууртай ба .

№3. Бүх утгыг ол Xпараметрийн дурын утгын хувьд А, интервалд хамааралгүй (0; 2], илэрхийлэл нь илэрхийлэлтэй тэнцүү биш байна. (USE-2007).

Асуудлыг дахин томъёолъё: "Бүх утгыг ол Xпараметрийн дурын утгын хувьд тэгшитгэл үндэсгүй."
илэрхийлье Адамжуулан X:

1) зөвшөөрөх. Дараа нь . Тиймээс тэгшитгэл нь үндэстэй. Энэ нь нөхцөлийг хангахгүй байна гэсэн үг юм.
2) үзье. Дараа нь . Координатын системийг ашиглацгаая ( xOa). (Зураг 3).

Нөхцөл байдал хангагдсан.

№4. Параметрээс хамаарч хэдэн үндэс Атэгшитгэл байна уу?

Модулийг өргөжүүлье:

Координатын системд ( xOy) функцын графикийг байгуулъя

тэгшитгэлээр өгөгдсөн зэрэгцээ шугамын харандааны хэд хэдэн мөр. (Зураг 4).

Хариулт: 1. Хэрэв , тэгвэл үндэс байхгүй болно.

2. Хэрэв , дараа нь нэг үндэс.

3. Хэрэв , хоёр үндэс байна.

IV.3. Параметртэй квадрат тэгш бус байдал

№5. Тэгш бус байдлыг шийд .

1 арга зам.

Үүнийг анхаарч үзье. Тэгвэл энэ тэгш бус байдлын шийдэл нь аль ч хүний ​​хувьд юм б.(Зураг 5).

Хэрэв , дараа нь бид тэгш бус байдал руу шилжих бөгөөд үүний шийдлийн багцыг координатын системд дүрсэлсэн болно ( хайрцаг). (Зураг 6).

Инжирийг нэгтгэцгээе. 5 ба 6.

Тэгээд одоо Зураг дагуу. 7, босоо шулуун шугамаар таслах нь хариултыг авахад хялбар байдаг.

Хариулт: 1. Хэрэв , тэгвэл .
2. Хэрэв , тэгвэл .
3. Хэрэв , тэгвэл

2 арга зам.

Координатын систем дэх тэгш бус байдлыг графикаар шийдье ( xOb):

. (Зураг 8).

Хоёр тохиолдлыг авч үзье.

1) . Дараа нь тэгш бус байдал нь хаана хэлбэртэй болно.
2) , дараа нь .

Функцийн график ба координатууд нь тэгш бус байдлыг хангадаг цэгүүдийг агуулсан хавтгайн хэсгийг Зураг 8-д үзүүлэв.

1. Хэрэв , тэгвэл .
2. Хэрэв , тэгвэл . 3. Хэрэв , тэгвэл .

3 арга зам.

Одоо координатын систем дэх график шийдлийг танилцуулъя ( xOy). Үүнийг хийхийн тулд модулийг өргөжүүлье:

Функцийг авч үзье .

Квадрат гурвалсан гишүүний үндэс .

Харьцуулъя ба .

1) , хаанаас .

Бид нийтийг нь авдаг. (Зураг 9)

2) , хаанаас . (Зураг 10).

Дараа нь өөрөөр хэлбэл. .

3) хаанаас . (Зураг 11).

Дараа нь өөрөөр хэлбэл. .

Хариулт: 1. Хэрэв , тэгвэл .

2. Хэрэв , тэгвэл .
3. Хэрэв , тэгвэл .

№6. Бүх параметрийн утгыг ол А, үүнд функцийн хамгийн бага утга 2-оос дээш.

Параметрийн бүх утгыг олоход хангалттай А, тус бүрийн хувьд тэгш бус байдал нь аль ч хувьд үнэн байна . Тэгш бус байдлыг хэлбэрээр дахин бичье ., ;

Тэгш бус байдал

(а, б, в, …,, x)>(a, b, c, …, x), (1)

хаана a, b, c, …,- параметрүүд ба x нь бодит хувьсагч бөгөөд нэг үл мэдэгдэх параметр агуулсан тэгш бус байдал гэнэ.

Аливаа параметрийн утгын систем a = a 0 , b = b 0 , c = c 0 , …, k = k 0 , зарим функцийн хувьд

(а, б, в, …,, x) ба

(а, б, в, …,, x

Зөвшөөрөгдөх параметрийн утгын систем гэж нэрлэгддэг бодит тоонуудын домэйнд утга учиртай.

х-ийн хүчинтэй утгыг if гэж нэрлэдэг

(а, б, в, …,, x) ба

(а, б, в, …,, x

параметрийн утгын зөвшөөрөгдөх аливаа системийн хүчинтэй утгыг авна.

X-ийн бүх зөвшөөрөгдөх утгуудын багцыг тэгш бус байдлын тодорхойлолтын домэйн гэж нэрлэдэг (1).

Бодит x 0 тоог тэгш бус байдлын хэсэгчилсэн шийдэл (1) гэж нэрлэдэг

(а, б, в, …,, x 0 )>(a, b, c, …, x 0 )

Зөвшөөрөгдөх параметрийн утгын аль ч системийн хувьд үнэн.

Тэгш бус байдлын бүх тодорхой шийдлүүдийн багцыг (1) энэ тэгш бус байдлын ерөнхий шийдэл гэнэ.

Тэгш бус байдлыг шийдвэрлэх (1) гэдэг нь параметрийн ямар утгуудад ерөнхий шийдэл байгаа, юу болохыг харуулахыг хэлнэ.

Хоёр тэгш бус байдал

(а, б, в, …,, x)>(a, b, c, …, x) ба (1)

(а, б, в, …,, x)>(a, b, c, …, x) (2)

Зөвшөөрөгдөх параметрийн утгуудын ижил багц системийн ерөнхий шийдэлтэй байвал тэдгээрийг эквивалент гэж нэрлэдэг.

Шийдлийн алгоритм.

Бид энэ тэгш бус байдлын тодорхойлолтын хүрээг олдог.

Бид тэгш бус байдлыг тэгшитгэл болгон бууруулна.

Бид a-г х-ийн функцээр илэрхийлнэ.

XOa координатын системд бид энэхүү тэгш бус байдлын тодорхойлолтод багтсан x-ийн утгуудын хувьд a = (x) функцүүдийн графикийг байгуулдаг.

Бид энэ тэгш бус байдлыг хангах цэгүүдийн багцыг олдог.

Үр дүнд үзүүлэх параметрийн нөлөөг авч үзье.

Графикуудын огтлолцох цэгүүдийн абсциссыг олъё.

a=const шулууныг тавиад --ээс + руу шилжүүлье

Бид хариултаа бичнэ.

Энэ бол xOa координатын системийг ашиглан параметртэй тэгш бус байдлыг шийдвэрлэх алгоритмуудын зөвхөн нэг юм. Стандарт xOy координатын системийг ашиглан шийдвэрлэх бусад аргууд бас боломжтой.

3. Жишээ

I. a параметрийн бүх зөвшөөрөгдөх утгуудын хувьд тэгш бус байдлыг шийд

Тэгш бус байдлын системээр тодорхойлогдсон a параметрийн тодорхойлолтын хүрээнд

энэ тэгш бус байдал нь тэгш бус байдлын системтэй тэнцүү байна

Хэрэв, анхны тэгш бус байдлын шийдлүүд интервалыг дүүргэнэ.

Хариулт:, .

II. a параметрийн ямар утгуудад систем шийдэлтэй байдаг вэ?

Тэгш бус байдлын зүүн талд гурвалсан язгуурыг олъё -

Тэгшитгэлээр (*) тодорхойлогдсон шулуун шугамууд aOx координатын хавтгайг дөрвөн мужид хуваадаг бөгөөд тус бүрт нь дөрвөлжин гурвалжин байдаг.

тогтмол тэмдгийг хадгалж байдаг. Тэгшитгэл (2) нь эх цэг дээр төвлөрсөн 2 радиустай тойргийг тодорхойлно. Дараа нь анхны системийн шийдэл нь сүүдэртэй огтлолцол байх болно

тойрог бүхий бүс, хаана болон утгууд нь системээс олддог

болон утгууд ба системээс олддог

Эдгээр системийг шийдэж, бид үүнийг олж авдаг

III. a параметрийн утгаас хамааран тэгш бус байдлыг шийд.

Бид хүлээн зөвшөөрөгдсөн утгын хүрээг олдог -

xOy координатын систем дэх функцийн графикийг байгуулъя.

тэгш бус байдлын шийдэл байхгүй үед.

шийдлийн хувьд x хамаарлыг хангах үед, хаана

Параметрээр тэгш бус байдлыг шийдвэрлэх.

ax > b, ax хэлбэртэй тэгш бус байдал< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются шугаман тэгш бус байдал.

Параметртэй шугаман тэгш бус байдлыг шийдвэрлэх зарчим нь параметртэй шугаман тэгшитгэлийг шийдвэрлэх зарчимтай маш төстэй юм.

Жишээ 1.

5x – a > ax + 3 тэгш бус байдлыг шийд.

Шийдэл.

Эхлээд анхны тэгш бус байдлыг хувиргая:

5x – ax > a + 3, тэгш бус байдлын зүүн талын хаалтнаас х-г гаргая:

(5 – a)x > a + 3. Одоо a параметрийн боломжит тохиолдлуудыг авч үзье:

Хэрэв a > 5 бол x< (а + 3) / (5 – а).

Хэрэв a = 5 бол шийдэл байхгүй болно.

Хэрвээ< 5, то x >(a + 3) / (5 - a).

Энэ шийдэл нь тэгш бус байдлын хариулт болно.

Жишээ 2.

a ≠ 1-ийн хувьд x(a – 2) / (a ​​– 1) – 2a/3 ≤ 2x – a тэгш бус байдлыг шийд.

Шийдэл.

Анхны тэгш бус байдлыг өөрчилье:

x(a – 2) / (a ​​– 1) – 2x ≤ 2a/3 – a;

Ах/(а – 1) ≤ -а/3. Тэгш бус байдлын хоёр талыг (-1) үржүүлснээр бид дараахь зүйлийг олж авна.

ax/(a – 1) ≥ a/3. a параметрийн боломжит тохиолдлуудыг авч үзье:

1 тохиолдол. a/(a – 1) > 0 эсвэл a € (-∞; 0)ᴗ(1; +∞) байг. Дараа нь x ≥ (a – 1)/3.

Тохиолдол 2. a/(a – 1) = 0, i.e. a = 0. Тэгвэл x нь дурын бодит тоо юм.

Тохиолдол 3. a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Хариулт: x € [(a – 1)/3; +∞) € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] € (0; 1);
a = 0-ийн хувьд x € R.

Жишээ 3.

|1 + x| тэгш бус байдлыг шийд ≤ сүх нь x-тэй харьцуулахад.

Шийдэл.

Тэгш бус байдлын сүхний баруун тал нь сөрөг биш байх ёстой гэсэн нөхцлөөс гарна. ax ≥ 0. |1 + x| тэгш бус байдлаас модулийг илрүүлэх дүрмээр ≤ сүх бидэнд давхар тэгш бус байдал байна

Сүх ≤ 1 + x ≤ сүх. Үр дүнг систем хэлбэрээр дахин бичье.

(сүх ≥ 1 + x;
(-сүх ≤ 1 + x.

Үүнийг өөрчилье:

((a – 1)x ≥ 1;
((a + 1)x ≥ -1.

Бид үүссэн системийг интервал болон цэгээр судалдаг (Зураг 1):

≤ -1 x € (-∞; 1/(a – 1)]-ийн хувьд.

-1-д< а < 0 x € [-1/(а – 1); 1/(а – 1)].

a = 0 x = -1 байх үед.

0-д< а ≤ 1 решений нет.

Тэгш бус байдлыг шийдвэрлэх график арга

График зурах нь параметр агуулсан тэгшитгэлийг шийдвэрлэхэд ихээхэн хялбар болгодог. Параметр бүхий тэгш бус байдлыг шийдвэрлэхдээ график аргыг ашиглах нь илүү тодорхой бөгөөд илүү тохиромжтой юм.

f(x) ≥ g(x) хэлбэрийн тэгш бус байдлыг графикаар шийднэ гэдэг нь f(x) функцийн график нь g(x) функцийн график дээр байрлах x хувьсагчийн утгыг олохыг хэлнэ. Үүнийг хийхийн тулд графикуудын огтлолцох цэгүүдийг (хэрэв байгаа бол) олох шаардлагатай байдаг.

Жишээ 1.

|x + 5| тэгш бус байдлыг шийд< bx.

Шийдэл.

y = |x + 5| функцийн графикийг байгуулна ба y = bx (Зураг 2). Тэгш бус байдлын шийдэл нь y = |x + 5| функцийн график байх x хувьсагчийн утгууд байх болно. y = bx функцийн графикаас доогуур байх болно.

Зурагт харуулав:

1) b > 1-ийн хувьд шугамууд огтлолцоно. Эдгээр функцүүдийн графикуудын огтлолцох цэгийн абсцисса нь x + 5 = bx тэгшитгэлийн шийдэл бөгөөд үүнээс x = 5/(b – 1) байна. y = bx график нь (5/(b – 1); +∞) интервалаас х дээр байрладаг бөгөөд энэ олонлог нь тэгш бус байдлын шийдэл юм.

2) Үүнтэй адилаар бид үүнийг -1-д олдог< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) b ≤ -1 x € (-∞; 5/(b – 1))-ийн хувьд.

4) 0 ≤ b ≤ 1-ийн хувьд графикууд огтлолцдоггүй бөгөөд энэ нь тэгш бус байдал нь шийдэлгүй гэсэн үг юм.

Хариулт: b ≤ -1-ийн хувьд x € (-∞; 5/(b – 1));
x € (-5/(b + 1); 5/(b - 1)) -1-д< b < 0;
0 ≤ b ≤ 1-ийн шийдэл байхгүй; b > 1-ийн хувьд x € (5/(b – 1); +∞).

Жишээ 2.

a(a + 1)x > (a + 1)(a + 4) тэгш бус байдлыг шийд.

Шийдэл.

1) a параметрийн "хяналтын" утгыг олцгооё: a 1 = 0, 2 = -1.

2) Энэ тэгш бус байдлыг бодит тооны дэд олонлог бүр дээр шийдье: (-∞; -1); (-1); (-10); (0); (0; +∞).

а) а< -1, из данного неравенства следует, что х >(a + 4)/a;

b) a = -1, тэгвэл энэ тэгш бус байдал 0 x > 0 хэлбэрийг авна – шийдэл байхгүй;

в) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, тэгвэл энэ тэгш бус байдал 0 x > 4 хэлбэртэй байна - шийдэл байхгүй;

e) a > 0, энэ тэгш бус байдлаас x > (a + 4)/a гарна.

Жишээ 3.

|2 – |x|| тэгш бус байдлыг шийд< a – x.

Шийдэл.

y = |2 – |x|| функцийн графикийг байгуулна (Зураг 3) y = -x + a шулуун шугамын байршлын бүх боломжит тохиолдлыг авч үзье.

Хариулт: тэгш бус байдал нь ≤ -2-ийн шийдэлгүй;
x € (-∞; (a – 2)/2) нь € (-2; 2];
a > 2 бол x € (-∞; (a + 2)/2).

Төрөл бүрийн асуудал, тэгшитгэл, параметр бүхий тэгш бус байдлыг шийдвэрлэхдээ олон тооны эвристик аргуудыг олж илрүүлж, дараа нь математикийн бусад салбаруудад амжилттай ашиглаж болно.

Параметртэй холбоотой асуудлууд нь логик сэтгэлгээ, математикийн соёлыг төлөвшүүлэхэд чухал үүрэг гүйцэтгэдэг. Тийм ч учраас параметртэй асуудлыг шийдвэрлэх аргуудыг эзэмшсэний дараа та бусад асуудлыг амжилттай даван туулах болно.

Асуулт хэвээр байна уу? Тэгш бус байдлыг хэрхэн шийдэхээ мэдэхгүй байна уу?
Багшаас тусламж авахын тулд -.
Эхний хичээл үнэ төлбөргүй!

blog.site, материалыг бүрэн эсвэл хэсэгчлэн хуулахдаа эх сурвалжийн холбоосыг оруулах шаардлагатай.