सत्य वेक्टर का उपयोग करके किसी फ़ंक्शन को निर्दिष्ट करना। पूर्ण बाइनरी ट्री का उपयोग करके निर्दिष्ट अदिश तर्क का वेक्टर फ़ंक्शन
मान लें कि अदिश तर्क के वेक्टर फ़ंक्शन के मानों के सेट को बिंदु 0 पर एक सामान्य मूल में घटा दिया गया है। आइए हम इस बिंदु के साथ कार्टेशियन समन्वय प्रणाली की उत्पत्ति का मिलान करें। फिर किसी भी वेक्टर को यूनिट वैक्टर में विस्तारित किया जा सकता है
इस प्रकार, एक अदिश तर्क के एक सदिश फलन को निर्दिष्ट करने का अर्थ है तीन अदिश फलनों को निर्दिष्ट करना 
जब तर्क का मान बदलता है, तो वेक्टर का अंत अंतरिक्ष में एक वक्र का वर्णन करेगा, जिसे वेक्टर होडोग्राफ़ कहा जाता है
चलो वहाँ के लिए एक करीबी मूल्य हो 
फिर एक अदिश तर्क के लिए एक सदिश फलन का व्युत्पन्न कहा जाता है 
क्रमांक 17 वक्ररेखीय गति में एक बिंदु की गति और त्वरण
रफ़्तार
वेग को किसी भौतिक बिंदु की गति की विशेषता के रूप में पेश किया जाता है। गति एक वेक्टर मात्रा है, जो एक निश्चित समय पर गति की गति (वेग वेक्टर परिमाण) और इसकी दिशा (वेग वेक्टर दिशा) दोनों की विशेषता है। मान लीजिए कि एक भौतिक बिंदु किसी वक्रीय प्रक्षेपवक्र के साथ चलता है, और समय t के क्षण में यह त्रिज्या वेक्टर r0 (छवि 1) से मेल खाता है। समय की एक छोटी अवधि Δt में, बिंदु Δs यात्रा करेगा और साथ ही एक प्राथमिक (असीमित) विस्थापन Δr प्राप्त करेगा।
औसत गति वेक्टर
औसत वेग वेक्टर की दिशा Δr की दिशा से मेल खाती है। Δt में अनंत कमी के साथ, औसत गति तात्कालिक गति v नामक मान की ओर प्रवृत्त होती है:
इसका मतलब यह है कि तात्कालिक गति v एक वेक्टर मात्रा है, जो समय के संबंध में गतिमान बिंदु के त्रिज्या वेक्टर के पहले व्युत्पन्न के बराबर है। क्योंकि सीमा में, छेदक स्पर्शरेखा के साथ मेल खाता है, फिर वेग वेक्टर v को गति की दिशा में प्रक्षेपवक्र के स्पर्शरेखा द्वारा निर्देशित किया जाता है (चित्र 2)।
अंक 2
जैसे-जैसे Δt घटता है, Δs तेजी से |Δr| तक पहुंचेगा, इसलिए तात्कालिक वेग मॉड्यूल
इसका मतलब यह है कि तात्कालिक गति का पूर्ण मान समय के संबंध में पथ के पहले व्युत्पन्न के बराबर है:
असमान गति के साथ, तात्कालिक वेग मॉड्यूल अलग-अलग समय पर भिन्न होता है। इस स्थिति में अदिश राशि का प्रयोग करें
यदि हम अभिव्यक्ति ds=vdt को समय के साथ t से t+Δt की सीमा में एकीकृत करते हैं (सूत्र (2) देखें), तो हम समय Δt के दौरान बिंदु द्वारा तय किए गए पथ की लंबाई ज्ञात करेंगे:
एकसमान गति के मामले में, तात्कालिक गति का संख्यात्मक मान स्थिर होता है; तब व्यंजक (3) रूप लेगा
t1 से t2 तक की समयावधि के दौरान एक बिंदु द्वारा तय किए गए पथ की लंबाई अभिन्न द्वारा दी गई है
त्वरण
असमान रूप से गाड़ी चलाते समय, अक्सर यह जानना आवश्यक होता है कि समय के साथ गति कितनी तेजी से बदलती है। वह भौतिक राशि जो परिमाण और दिशा में गति में परिवर्तन की दर को दर्शाती है, त्वरण कहलाती है। आइए हम समतल गति पर विचार करें - वह गति जिसमें विचाराधीन प्रणाली के प्रत्येक बिंदु के प्रक्षेप पथ एक ही तल में होते हैं। मान लीजिए वेक्टर v समय t पर बिंदु A की गति है। समय Δt के दौरान, बिंदु स्थिति B पर चला गया और परिमाण और दिशा दोनों में v से भिन्न और v1 + Δv के बराबर गति प्राप्त की। आइए वेक्टर v1 को बिंदु A पर ले जाएं और Δv ढूंढें (चित्र 1)।
T से t+Δt के अंतराल में असमान गति का औसत त्वरण एक वेक्टर मात्रा है जो गति Δv में परिवर्तन और समय अंतराल Δt के अनुपात के बराबर है:
समय t पर किसी भौतिक बिंदु का तात्कालिक त्वरण a (त्वरण) एक सदिश राशि होगी:
समय के संबंध में गति के प्रथम व्युत्पन्न के बराबर।
आइए वेक्टर Δv को दो घटकों में विघटित करें। ऐसा करने के लिए, बिंदु A (चित्र 1) से वेग v की दिशा में, हम वेक्टर AD आलेखित करते हैं, जिसका मापांक v1 के बराबर है। जाहिर है, Δvτ के बराबर सीडी वेक्टर समय के साथ गति में परिवर्तन को निर्धारित करता है: Δt मॉड्यूल: Δvτ=v1-v। वेक्टर Δv का दूसरा घटक Δvn समय के साथ दिशा में गति में परिवर्तन को दर्शाता है।
त्वरण का स्पर्शरेखीय घटक:
यानी, यह गति मापांक के समय के संबंध में पहले व्युत्पन्न के बराबर है, जिससे मापांक में गति के परिवर्तन की दर निर्धारित होती है।
हम त्वरण के दूसरे घटक की तलाश कर रहे हैं। हम मानते हैं कि बिंदु B, बिंदु A के बहुत करीब है, इसलिए Δs को कुछ त्रिज्या r के एक वृत्त का चाप माना जा सकता है, जो जीवा AB से थोड़ा अलग है। त्रिभुज AOB त्रिभुज EAD के समान है, जिससे यह Δvn/AB=v1/r का अनुसरण करता है, लेकिन चूँकि AB=vΔt है, तो
Δt→0 की सीमा में हमें v1→v प्राप्त होता है।
क्योंकि v1→v, कोण EAD शून्य की ओर प्रवृत्त होता है, और तब से त्रिभुज EAD समद्विबाहु है, तो v और Δvn के बीच का कोण ADE समकोण की ओर प्रवृत्त होता है। परिणामस्वरूप, Δt→0 पर सदिश Δvn और v परस्पर लंबवत हो जाते हैं। क्योंकि वेग वेक्टर को प्रक्षेपवक्र के स्पर्शरेखीय रूप से निर्देशित किया जाता है, फिर वेक्टर Δvn, वेग वेक्टर के लंबवत, बिंदु के प्रक्षेपवक्र के वक्रता केंद्र की ओर निर्देशित किया जाता है। त्वरण का दूसरा घटक, के बराबर
इसे त्वरण का सामान्य घटक कहा जाता है और इसकी वक्रता के केंद्र के प्रक्षेपवक्र (जिसे सामान्य कहा जाता है) के स्पर्शरेखा के लंबवत सीधी रेखा के साथ निर्देशित किया जाता है (इसलिए इसे सेंट्रिपेटल त्वरण भी कहा जाता है)।
पिंड का कुल त्वरण स्पर्शरेखीय और सामान्य घटकों का ज्यामितीय योग है (चित्र 2):
इसका मतलब यह है कि त्वरण का स्पर्शरेखीय घटक परिमाण में गति में परिवर्तन की दर (प्रक्षेपवक्र की ओर निर्देशित) की एक विशेषता है, और त्वरण का सामान्य घटक दिशा में गति में परिवर्तन की दर की एक विशेषता है (की ओर निर्देशित) प्रक्षेपवक्र की वक्रता का केंद्र)। त्वरण के स्पर्शरेखा और सामान्य घटकों के आधार पर, गति को निम्नानुसार वर्गीकृत किया जा सकता है:
1)aτ=0, an=0 - सीधीरेखीय एकसमान गति;
2)aτ=an=const, аn=0 - सीधीरेखीय एकसमान गति। इस प्रकार के आंदोलन के साथ
यदि प्रारंभिक समय t1 = 0, और प्रारंभिक गति v1 = v0, तो, t2=t और v2 = v को दर्शाते हुए, हम a=(v-v0)/t प्राप्त करते हैं, जिससे
इस सूत्र को शून्य से लेकर समय के एक मनमाने क्षण टी तक की सीमा में एकीकृत करने पर, हम पाते हैं कि समान रूप से परिवर्तनशील गति के मामले में एक बिंदु द्वारा तय किए गए पथ की लंबाई
3)aτ=f(t), an=0 - परिवर्तनशील त्वरण के साथ सीधी गति;
4)aτ=0, an=const. जब aτ=0, गति निरपेक्ष मान में नहीं बदलती, बल्कि दिशा में बदलती है। सूत्र an=v2/r से यह निष्कर्ष निकलता है कि वक्रता त्रिज्या स्थिर होनी चाहिए। इसलिए, वृत्ताकार गति एकसमान है; एकसमान वक्ररेखीय गति;
5)aτ=0, an≠0 एकसमान वक्ररेखीय गति;
6)aτ=const, an≠0 - वक्ररेखीय एकसमान गति;
7)aτ=f(t), an≠0 - परिवर्तनशील त्वरण के साथ वक्ररेखीय गति।
क्रमांक 18 स्पर्शरेखा तल और सतह के अभिलम्ब के समीकरण
परिभाषा। मान लें कि डोमेन D पर दो चर z =f(x,y) का एक फ़ंक्शन दिया गया है, M0(x0;y0) डोमेन D का एक आंतरिक बिंदु है, M(x0+Δx;y+Δy) एक बिंदु है डी "पड़ोसी" M0.
फ़ंक्शन की पूर्ण वृद्धि पर विचार करें:
यदि Δz को इस प्रकार दर्शाया गया है:
जहां A, B स्थिरांक हैं (Δx, Δy से स्वतंत्र), 
- एम और एम0 के बीच की दूरी, α(Δ x,Δy) - Δx 0, Δy 0 पर अतिसूक्ष्म; तब फ़ंक्शन z =f(x,y) को बिंदु M0 पर अवकलनीय कहा जाता है, और अभिव्यक्ति
बिंदु M0 पर फ़ंक्शन z =f(x;y) का कुल अंतर कहा जाता है।
प्रमेय 1.1. यदि z =f(x;y) बिंदु M0 पर अवकलनीय है, तो
सबूत
चूँकि (1.16) में Δx, Δy मनमाना अनंतिम हैं, हम Δy =0, Δx≠0, Δx 0 ले सकते हैं, फिर
जिसके बाद (1.16) से यह अनुसरण करता है
इसी प्रकार यह भी सिद्ध हो गया है
और प्रमेय 1.1. सिद्ध किया हुआ।
ध्यान दें: बिंदु M0 पर z =f(x,y) की भिन्नता आंशिक व्युत्पन्न के अस्तित्व को दर्शाती है। विपरीत कथन गलत है (बिंदु M0 पर आंशिक व्युत्पन्न का अस्तित्व बिंदु M0 पर भिन्नता का संकेत नहीं देता है)।
परिणामस्वरूप, प्रमेय 1.1 को ध्यान में रखते हुए, सूत्र (1.18) रूप लेगा:
परिणाम। बिंदु M0 पर अवकलनीय एक फ़ंक्शन इस बिंदु पर निरंतर है (क्योंकि (1.17) से यह पता चलता है कि Δx 0, Δy 0 के लिए: Δz 0, z(M) z(M0))।
नोट: इसी प्रकार तीन या अधिक चर के मामले के लिए। अभिव्यक्ति (1.17) का रूप लेगा:
आंशिक व्युत्पन्न के ज्यामितीय अर्थ (चित्र 1.3) का उपयोग करके, हम सतह पर स्पर्शरेखा विमान πcass के निम्नलिखित समीकरण (1.24) प्राप्त कर सकते हैं: z =f(x,y) बिंदु C0(x0,y0,z0) पर, z0=z(M):
(1.24) और (1.21) की तुलना से हम दो चर के एक फ़ंक्शन के कुल अंतर का ज्यामितीय अर्थ प्राप्त करते हैं:
जब बिंदु C, बिंदु C0 से बिंदु तक स्पर्शरेखा तल के अनुदिश गति करता है तो अनुप्रयुक्त z की वृद्धि
कहाँ से है (1.24).
सतह पर सामान्य Lн का समीकरण: बिंदु C0 पर z = f(x,y) स्पर्शरेखा तल के लंबवत C0 से गुजरने वाली एक सीधी रेखा के समीकरण के रूप में प्राप्त किया जाता है:
क्रमांक 19 दिशात्मक व्युत्पन्न। ढाल
मान लीजिए कि किसी डोमेन में कोई फ़ंक्शन दिया गया है 
और अवधि 
. आइए उस बिंदु से एक सदिश बनाएं जिसकी दिशा कोज्या है 
. वेक्टर पर, इसकी शुरुआत से कुछ दूरी पर, एक बिंदु पर विचार करें, अर्थात। .
हम यह मान लेंगे कि function और इसके प्रथम-क्रम आंशिक व्युत्पन्न डोमेन में निरंतर हैं।
अनुपात की सीमा को फ़ंक्शन का व्युत्पन्न कहा जाता है बिंदु पर वेक्टर की दिशा में और निरूपित किया जाता है, अर्थात। .
किसी फ़ंक्शन का व्युत्पन्न ज्ञात करना किसी दिए गए बिंदु पर 
वेक्टर की दिशा में 
सूत्र का उपयोग करें:
कहाँ – वेक्टर की दिशा कोसाइन , जिनकी गणना सूत्रों द्वारा की जाती है: 
.
मान लीजिए किसी निश्चित क्षेत्र के प्रत्येक बिंदु पर एक फ़ंक्शन निर्दिष्ट किया गया है .
एक वेक्टर जिसके निर्देशांक अक्षों पर प्रक्षेपण संबंधित बिंदु पर इस फ़ंक्शन के आंशिक व्युत्पन्न के मान होते हैं, फ़ंक्शन का ग्रेडिएंट कहलाता है और निर्दिष्ट है या ("नबला यू" पढ़ें): .
इस मामले में, वे कहते हैं कि क्षेत्र में ग्रेडिएंट्स का एक वेक्टर क्षेत्र परिभाषित किया गया है।
किसी फ़ंक्शन का ग्रेडिएंट ढूँढने के लिए किसी दिए गए बिंदु पर सूत्र का उपयोग करें: .
संख्या 22 अनिश्चितकालीन अभिन्न के मूल गुण
अनिश्चितकालीन अभिन्न
जहां F फ़ंक्शन f (अंतराल पर) का प्रतिअवकलज है; C एक मनमाना स्थिरांक है।
बुनियादी गुण
1. 
2. 
3. यदि 
वह
24) 
25) 
28) 
इस पद्धति का उपयोग उन मामलों में किया जाता है जहां इंटीग्रैंड विषम कार्यों का उत्पाद या भागफल होता है। इस मामले में, V'(x) को वह हिस्सा माना जाता है जो आसानी से एकीकृत हो जाता है।
29) 
32) एक परिमेय भिन्न का सरल भिन्नों में अपघटन.
कोई उचित तर्कसंगत अंश 
पहले-चौथे प्रकार के सरल तर्कसंगत भिन्नों की एक सीमित संख्या के योग के रूप में दर्शाया जा सकता है। विघटन के लिए हर को सरल भिन्नों में विस्तारित करना आवश्यक है क्यूएम(एक्स)रैखिक और वर्ग गुणनखंडों में, जिसके लिए आपको समीकरण को हल करना होगा:
- (5)
प्रमेय.उचित तर्कसंगत भिन्न , कहाँ 
, सरल भिन्नों के योग में विशिष्ट रूप से विघटित किया जा सकता है:
- (6)
(ए 1, ए 2, …, ए के, बी 1, बी 2, …, बी 1, एम 1, एन 1, एम 2, एम 2, …, एम एस, एन एस - कुछ वास्तविक संख्याएं)।
33) हर की जटिल जड़ों के साथ एक उचित भिन्न को सरल भिन्नों में विघटित करना
समस्या का निरूपण. अनिश्चितकालीन अभिन्न खोजें
1 . आइए निम्नलिखित संकेतन का परिचय दें:
आइए अंश और हर की डिग्री की तुलना करें।
यदि समाकलन एक अनुचित परिमेय भिन्न है, अर्थात अंशांकक डिग्रीएन हर की घात से अधिक या उसके बराबरएम , तो पहले हम अंश को हर से विभाजित करके परिमेय फलन के पूरे भाग का चयन करते हैं:
यहाँ बहुपद विभाजन और घात का शेषफल हैपीके(एक्स) कम डिग्रीक्यूएम
2 . आइए उचित परिमेय भिन्न का विस्तार करें
प्राथमिक भिन्नों के लिए.
यदि इसके हर में सरल जटिल जड़ें हैं यानी
फिर विस्तार का रूप है
3 . अनिश्चित गुणांकों की गणना करने के लिए,A1,A2,A3...B1,B1,B3... हम पहचान के दाईं ओर के भिन्न को एक सामान्य हर में लाते हैं, जिसके बाद हम समान घातों पर गुणांकों को बराबर करते हैंएक्स बाएँ और दाएँ अंशों में। आइए सिस्टम प्राप्त करें 2 एस के साथ समीकरण 2 एस अज्ञात, जिसका एक अनोखा समाधान है।
4 हम फॉर्म के प्राथमिक अंशों को एकीकृत करते हैं
47) यदि λ → 0 के रूप में अभिन्न योग की एक परिमित सीमा I है, और यह बिंदु ξ i चुनने की विधि, खंड को विभाजित करने की विधि पर निर्भर नहीं है, तो इस सीमा को फ़ंक्शन f का निश्चित अभिन्न अंग कहा जाता है ( x) खंड पर है और इसे इस प्रकार दर्शाया गया है:
इस मामले में, फ़ंक्शन f (x) को पूर्णांक कहा जाता है। संख्या ए और बी को क्रमशः एकीकरण की निचली और ऊपरी सीमा कहा जाता है, एफ (एक्स) इंटीग्रैंड है, एक्स एकीकरण का चर है। यह ध्यान दिया जाना चाहिए कि इससे कोई फर्क नहीं पड़ता कि कौन सा अक्षर एक निश्चित अभिन्न अंग के एकीकरण चर को दर्शाता है
चूँकि इस प्रकार के नोटेशन बदलने से किसी भी तरह से अभिन्न योग के व्यवहार पर कोई प्रभाव नहीं पड़ता है। संकेतन और शब्दावली में समानता के बावजूद, निश्चित और अनिश्चित अभिन्न भिन्न होते हैं
48) एक निश्चित अभिन्न के अस्तित्व पर प्रमेय
आइए खंड को बिंदुओं x1,x2,x3... द्वारा भागों में विभाजित करें
आइए हम डेल्टाएक्स द्वारा आई-वें टुकड़े की लंबाई और इन लंबाई की अधिकतम लंबाई को निरूपित करें।
आइए हम मनमाने ढंग से प्रत्येक खंड पर एक निश्चित बिंदु का चयन करें ताकि (इसे "मध्यबिंदु" कहा जाए), और लिखें
एक मात्रा जिसे अभिन्न योग कहा जाता है
आइए अब सीमा ज्ञात करें
परिभाषा। यदि यह अस्तित्व में है और यह इस पर निर्भर नहीं है
a) किसी खंड को भागों में और से विभाजित करने की विधि
बी) मध्यबिंदु चुनने की विधि,
खंड पर फ़ंक्शन f(x) का एक निश्चित अभिन्न अंग है।
इस मामले में फ़ंक्शन f(x) को अंतराल पर समाकलनीय कहा जाता है। मात्रा a और b को क्रमशः एकीकरण की निचली और ऊपरी सीमाएँ कहा जाता है।
50) एक निश्चित अभिन्न के मूल गुण
1) यदि एकीकरण अंतराल को आंशिक अंतरालों की एक सीमित संख्या में विभाजित किया जाता है, तो अंतराल पर लिया गया निश्चित अभिन्न उसके सभी आंशिक अंतरालों पर लिए गए निश्चित अभिन्नों के योग के बराबर होता है।
2) माध्य मान प्रमेय.
मान लें कि फ़ंक्शन y = f(x) अंतराल पर पूर्णांकित है, m=min f(x) और M=max f(x), तो ऐसी संख्या मौजूद है
परिणाम।
यदि फ़ंक्शन y = f(x) अंतराल पर निरंतर है, तो ऐसी एक संख्या है।
3) एकीकरण की सीमाओं को पुनर्व्यवस्थित करते समय, निश्चित अभिन्न अपना चिह्न विपरीत में बदल देता है।
4) एकीकरण की समान सीमा वाला एक निश्चित अभिन्न अंग शून्य के बराबर होता है।
5)फ़ंक्शन मॉड्यूल का एकीकरण
यदि फ़ंक्शन f(x) समाकलनीय है, तो इसका मॉड्यूल भी अंतराल पर समाकलनीय है।
6)असमानता का एकीकरण
यदि f(x) और q(x) एक अंतराल पर समाकलनीय हैं और x का संबंध है
वह
7)रैखिकता
अचर गुणनखंड को निश्चित समाकलन के चिह्न से परे ले जाया जा सकता है
यदि f(x) मौजूद है और अंतराल पर पूर्णांकीय है, A=const
यदि फलन y=f(x) एक अंतराल पर सतत है और F(x) (F'(x)=f(x)) पर इसका कोई प्रतिअवकलन है, तो सूत्र मान्य है
मान लीजिए कि एक सतत फलन के समाकलन की गणना के लिए प्रतिस्थापन x=α(t) किया जाता है।
1) फ़ंक्शन x=α(t) और इसका व्युत्पन्न x'=α'(t) t से संबंधित के लिए निरंतर हैं
2) t पर फ़ंक्शन x=α(t) के मानों का सेट सेगमेंट से संबंधित है
3) A α(c)=a और α(v)=b
मान लीजिए कि फ़ंक्शन f(x) अंतराल पर निरंतर है और x=b पर अनंत असंततता है। यदि कोई सीमा मौजूद है, तो इसे दूसरे प्रकार का अनुचित अभिन्न अंग कहा जाता है और इसे द्वारा दर्शाया जाता है।
इस प्रकार, परिभाषा के अनुसार,
यदि दाहिनी ओर की सीमा मौजूद है, तो अनुचित अभिन्न अंग जुटता है.यदि निर्दिष्ट सीमा अस्तित्व में नहीं है या अनंत है, तो वे कहते हैं कि अभिन्न विचलन
और इसका भेदभाव.
स्थानिक वक्र निर्दिष्ट करने के सबसे सरल तरीकों में से एक वेक्टर समीकरण निर्दिष्ट करना है:
कहाँ 
वक्र बिंदु का त्रिज्या वेक्टर है, और 
- पैरामीटर जो बिंदु की स्थिति निर्धारित करता है।
वह। परिवर्तनशील सदिश 
एक अदिश फलन है 
. गणितीय विश्लेषण में, ऐसे कार्यों को अदिश तर्क के सदिश फलन कहा जाता है।
सड़ते 
यूनिट वैक्टर का उपयोग करके, समीकरण (1) को फॉर्म दिया जा सकता है:
यह विस्तार वक्र के पैरामीट्रिक समीकरण पर आगे बढ़ना संभव बनाता है:
दूसरे शब्दों में, एक वेक्टर फ़ंक्शन निर्दिष्ट करना तीन अदिश फ़ंक्शन निर्दिष्ट करने के बराबर है।
इस वक्र को परिभाषित करने वाले वेक्टर फ़ंक्शन (1) के संबंध में, वक्र को ही इस फ़ंक्शन का होडोग्राफ़ कहा जाता है। इस मामले में निर्देशांक की उत्पत्ति को होडोग्राफ का ध्रुव कहा जाता है।
अभी रहने दो 
और 
- समीकरण (1) द्वारा परिभाषित वक्र के बिंदु। इसके अतिरिक्त 
, ए 
इन बिंदुओं के त्रिज्या सदिश होंगे
और 
.
वेक्टर 
वेक्टर फ़ंक्शन की वृद्धि कहा जाता है 
, वेतन वृद्धि के अनुरूप 
इसका तर्क, और द्वारा निरूपित किया जाता है 
,
वेक्टर फ़ंक्शन 
एक सतत कार्य होगा 
, अगर
.
का व्युत्पन्न ज्ञात करना 
आइए निम्नानुसार आगे बढ़ें -
.
आइए अब दिशा तय करें 
. यह तो स्पष्ट है 
के साथ संरेख 
और कम से 
उसी दिशा में निर्देशित किया गया है 
और जब 
- विपरीत दिशा में। लेकिन पहले मामले में 
और दूसरे में 
वह। वेक्टर 
हमेशा सेकेंट होडोग्राफ के साथ निर्देशित 
ऊपर की ओर 
.
यदि हम विस्तार का उपयोग करते हैं 
और 
ओर्ट्स द्वारा, फिर
यहाँ से (*) को विभाजित करने पर 
और सीमा तक जा रहे हैं 
के लिए 
हम पाते हैं
(4) के आधार पर, यह दिखाया जा सकता है कि निम्नलिखित सूत्र मान्य हैं:
(5) 
(6) 
- अदिश फलन.
प्रमाण (7).
आइए अब कुछ संपत्तियों की जांच करें 
. सबसे पहले, आइए इसका मॉड्यूल खोजें:
.
क्योंकि हम होडोग्राफ आर्क को सुधार योग्य मानते हैं 
- तार की लंबाई है, और 
- वक्राकार लंबाई। इसीलिए
वह। एक अदिश तर्क के सदिश फलन के व्युत्पन्न का मापांक उसी तर्क के संबंध में होडोग्राफ चाप के व्युत्पन्न के बराबर होता है।
परिणाम 1. यदि 
- यूनिट वेक्टर वृद्धि की दिशा में होडोग्राफ के स्पर्शरेखीय रूप से निर्देशित है 
, वह
परिणाम 2. यदि होडोग्राफ़ चाप की लंबाई को वेक्टर फ़ंक्शन के तर्क के रूप में लिया जाता है 
, वह
(क्योंकि 
)
वह। होडोग्राफ के चाप की लंबाई के साथ वेक्टर फ़ंक्शन का व्युत्पन्न होडोग्राफ के स्पर्शरेखा के इकाई वेक्टर के बराबर है, जो चाप की लंबाई बढ़ाने की दिशा में निर्देशित है।
उपफल 3. यदि किसी सदिश फलन के होडोग्राफ को एक बिंदु का प्रक्षेपवक्र माना जाता है, और 
- आंदोलन के समय के रूप में, एक निश्चित से गिना जाता है 
, वह 
गति वेग वेक्टर के साथ परिमाण और दिशा में मेल खाता है 
.
वास्तव में, गति का अदिश मान समय के संबंध में पथ के व्युत्पन्न के बराबर है:
इसके अलावा वेक्टर 
गति की दिशा में प्रक्षेपवक्र के स्पर्शरेखीय रूप से निर्देशित, जो वृद्धि की दिशा से मेल खाती है 
, अर्थात। दिशा के अनुरूप है 
.
वह। 
.
आइये अब विचार करें 
, जिसकी लंबाई स्थिर है, 
, अर्थात।
(*) 
कहाँ 
(*) को विभेदित करने पर, हम पाते हैं:
वे। 
विशेष रूप से, इकाई की दिशा में किसी भी चर के वेक्टर का व्युत्पन्न 
हमेशा 
.
अभी रहने दो 
बिंदुओं पर खींचे गए इकाई गोले की त्रिज्याओं के बीच का कोण 
और 
hodograph 
. फिर तार की लंबाई 
एक त्रिकोण से 
बराबर होगा
एक इकाई चर वेक्टर के व्युत्पन्न का परिमाण इस वेक्टर के घूर्णन के कोणीय वेग के बराबर है।
जहाँ तक अदिश फलनों का प्रश्न है, एक सदिश फलन का अंतर इस प्रकार लिखा जाता है
किंतु इसके बावजूद
एक स्थानिक वक्र की वक्रता.
साथ में त्रिफलक।
परिणाम 2 के अनुसार, के लिए 
हम सूत्र लिख सकते हैं:
दिशा बदलना 
, स्थानिक वक्र के स्पर्शरेखा में परिवर्तन के साथ जुड़ा हुआ, वक्र की वक्रता को दर्शाता है। एक स्थानिक वक्र की वक्रता के माप के रूप में, एक समतल वक्र की तरह, चाप की लंबाई के निकटवर्ती कोण के अनुपात की सीमा ली जाती है, जब 
वक्रता, 
आसन्न कोण, 
वक्राकार लंबाई।
दूसरी ओर, 
यूनिट वेक्टर और उसका व्युत्पन्न वेक्टर 
इसके लंबवत है, और इसका मापांक 
फर्क 
द्वारा 
और प्रवेश कर रहा हूँ 
दिशा के साथ यूनिट वेक्टर 
, हम देखतें है:
वेक्टर 
अंतरिक्ष वक्र का वक्रता वेक्टर। इसकी दिशा, स्पर्शरेखा दिशा के लंबवत, अंतरिक्ष वक्र की सामान्य दिशा है। लेकिन एक स्थानिक वक्र में किसी भी बिंदु पर अनंत संख्या में सामान्य होते हैं, जो सभी वक्र के दिए गए बिंदु से गुजरने वाले विमान में स्थित होते हैं और किसी दिए गए बिंदु पर स्पर्शरेखा के लंबवत होते हैं। इस तल को स्थानिक वक्र का सामान्य तल कहा जाता है।
परिभाषा। वक्र का सामान्य जिसके अनुदिश वक्र का वक्रता वेक्टर किसी दिए गए बिंदु पर निर्देशित होता है, स्थानिक वक्र का मुख्य सामान्य होता है। वह। 
इकाई प्रमुख सामान्य वेक्टर.
आइए अब तीसरी इकाई वेक्टर का निर्माण करें 
क्रॉस उत्पाद के बराबर 
और 
वेक्टर 
, साथ ही 
लंबवत भी 
वे। सामान्य तल में स्थित है। इसकी दिशा को किसी दिए गए बिंदु पर स्थानिक वक्र के द्विअसामान्य की दिशा कहा जाता है। वेक्टर 
और 
परस्पर लंबवत इकाई वैक्टर की एक तिकड़ी का गठन करें, जिसकी दिशा स्थानिक वक्र पर बिंदु की स्थिति पर निर्भर करती है और बिंदु से बिंदु तक भिन्न होती है। ये वैक्टर तथाकथित बनाते हैं। एक स्थानिक वक्र के साथ ट्राइहेड्रॉन (फ्रेनेट ट्राइहेड्रॉन)। वेक्टर 
और 
यूनिट यूनिट वैक्टर की तरह, एक सही ट्रिपल बनाएं 
सही समन्वय प्रणाली में.
जोड़े में लिया गया 
वक्र पर एक ही बिंदु से गुजरने वाले और साथ वाले ट्राइहेड्रॉन के चेहरे बनाने वाले तीन विमानों को परिभाषित करें। जिसमें 
और 
ऑस्कुलेटिंग विमान का निर्धारण करें (किसी दिए गए बिंदु के आसपास के क्षेत्र में एक वक्र का चाप उच्च क्रम की सटीकता के लिए ऑस्कुलेटिंग विमान में एक विमान वक्र का चाप है);
और 
- सीधा विमान;
और 
- सामान्य विमान.
स्पर्शरेखा, सामान्य और द्विअसामान्य समीकरण।
संलग्न त्रिफलक के तलों के समीकरण।
जानने 
और 
, या कोई गैर-इकाई सदिश उनके समरेख में टी,एनऔर बीआइए हम इस खंड में नामित समीकरण प्राप्त करें।
ऐसा करने के लिए, सीधी रेखा के विहित समीकरण में
और किसी दिए गए बिंदु से गुजरने वाले विमान के समीकरण में
के लिए ले 
वक्र पर चयनित बिंदु के निर्देशांक, के लिए 
या क्रमशः के लिए 
सदिशों के निर्देशांक लीजिए 
या 
, जो वांछित रेखा की दिशा या वांछित तल के अभिलम्ब को निर्धारित करता है:
या 
- स्पर्शरेखा या सामान्य तल के लिए,
या 
- मुख्य सामान्य और सीधा करने वाले तल के लिए,
या 
- द्विअसामान्य और ऑस्कुलेटिंग विमान के लिए।
यदि वक्र सदिश समीकरण द्वारा दिया गया है 
या 
फिर वेक्टर के लिए 
प्रत्यक्ष रूप से निर्देशित किया जा सकता है 
ढूँढ़ने के लिए 
और 
आइए सबसे पहले अपघटन का पता लगाएं 
वैक्टर द्वारा 
पहले (परिणाम 1) हमने वह पाया था 
द्वारा विभेद करना 
, हम पाते हैं:
लेकिन क्योंकि 
आइए अब सदिश रूप से गुणा करें 
और 
(*) 
प्रति वेक्टर (*) के आधार पर 
, एक द्विअसामान्य दिशा होने पर, हम वेक्टर ले सकते हैं
लेकिन फिर, के लिए 
हम इन उत्तरार्द्ध का वेक्टर उत्पाद ले सकते हैं:
वह। एक मनमाना वक्र पर किसी भी बिंदु पर हम संलग्न त्रिफलक के सभी तत्वों को निर्धारित कर सकते हैं।
उदाहरण। किसी भी बिंदु पर दाएँ हेलिक्स के स्पर्शरेखा, सामान्य और द्विअसामान्य का समीकरण।
स्पर्शरेखा 
घर सामान्य 
द्विसामान्य 
डिपॉज़िटफ़ाइल्स से डाउनलोड करें
विभेदक ज्यामिति
मैं. अदिश तर्क का वेक्टर फलन
वेक्टर फ़ंक्शन (परिभाषा 1.1), इसे निर्दिष्ट करने की विधियाँ।
त्रिज्या वेक्टर और होडोग्राफ, पैरामीट्रिक होडोग्राफ विशिष्टता।
एक वेक्टर फ़ंक्शन का व्युत्पन्न (परिभाषा 1.6)।
एक वेक्टर फ़ंक्शन के व्युत्पन्न का ज्यामितीय अर्थ।
सदिश फलनों के विभेदन के नियम।
1.1. वेक्टर फ़ंक्शन की परिभाषा
परिभाषा 1.1यदि अदिश तर्क का प्रत्येक मानमिलान वेक्टर 
त्रि-आयामी स्थानआर 3 , तो वे कहते हैं कि सेट एक्स पर एक स्केलर तर्क का एक वेक्टर फ़ंक्शन (या वेक्टर फ़ंक्शन) दिया गया हैटी
.
यदि अंतरिक्ष मेंआर 3 एक कार्टेशियन समन्वय प्रणाली निर्दिष्ट हैके बारे में
xyz
, तो कार्य एक वेक्टर-फ़ंक्शन है 
, 
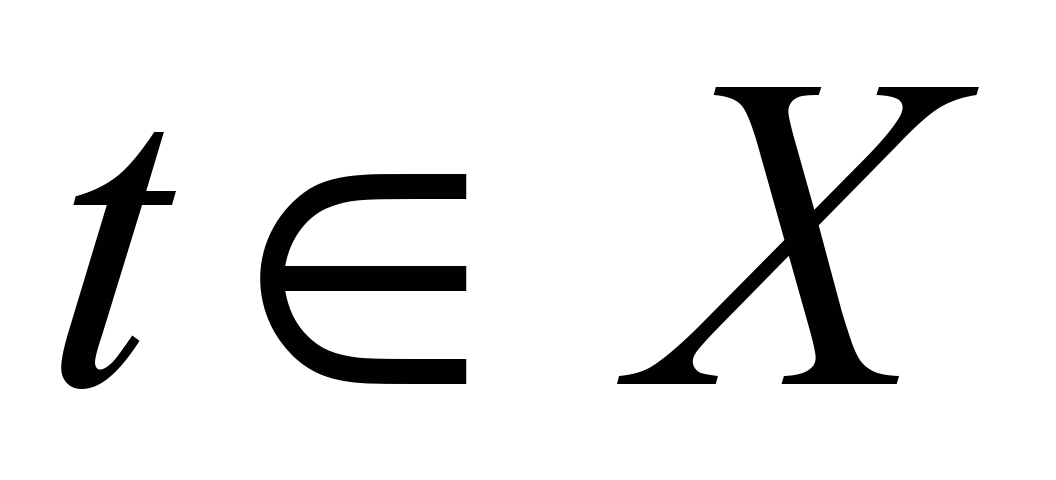तीन अदिश फलनों को निर्दिष्ट करने के बराबर हैएक्स(
टी
),
य
(
टी
),
जेड
(
टी
)
– वेक्टर निर्देशांक:
= { एक्स ( टी ), य ( टी ), जेड ( टी )} (1.1)
या , (1.2)
कहाँ 
- इकाई सदिशों का समन्वय करें।
1.2. त्रिज्या वेक्टर के होडोग्राफ के रूप में स्थानिक रेखा
परिभाषा 1.2 यदि सभी वैक्टरों की शुरुआत है,मूल बिंदु पर रखे जाने पर, उन्हें त्रिज्या सदिश कहा जाता है।
परिभाषा 1.3 वह रेखा जो त्रिज्या सदिशों के सिरों का ज्यामितीय स्थान है, सदिश फलन का होडोग्राफ कहलाती है, और उनकी सामान्य शुरुआत होडोग्राफ पोल है।
यदि पैरामीटर टी समय है, और गतिमान बिंदु का त्रिज्या वेक्टर है, तो फ़ंक्शन का होडोग्राफ गतिमान बिंदु का प्रक्षेपवक्र है।
होडोग्राफ़ समीकरण वेक्टर रूप (1.2) या पैरामीट्रिक रूप में लिखा जा सकता है:
(1.3)
विशेष रूप से, यदि वेक्टर फ़ंक्शनतर्क में बदलाव के साथ, केवल इसका मॉड्यूल बदलता है, लेकिन दिशा नहीं बदलती (), तो ऐसे वेक्टर फ़ंक्शन का होडोग्राफ मूल से निकलने वाली एक सीधी किरण होगी; यदि केवल वेक्टर की दिशा बदलती है, लेकिन इसका परिमाण अपरिवर्तित रहता है ( 
), तो वेक्टर फ़ंक्शन का होडोग्राफ एक गोले पर स्थित एक वक्र होगा जिसका केंद्र ध्रुव पर होगा और त्रिज्या वेक्टर के निरंतर मापांक के बराबर होगी।
चित्र 1।
1.3. वेक्टर-फ़ंक्शन की सीमा, निरंतरता और व्युत्पन्न
परिभाषा 1. 4 वेक्टर 
सदिश फलन की सीमा कहलाती हैपर 
, अगर
.
(1.4)
परिभाषा 1.5वेक्टर फ़ंक्शन को कहा जाता है एक बिंदु पर निरंतरटी 0, यदि इस बिंदु पर इसकी सीमा इस बिंदु पर वेक्टर फ़ंक्शन के मान के बराबर है:
. (1.5)
परिभाषा 1.6एक सदिश फलन का व्युत्पन्नबिंदु पर टी
किसी सदिश फलन की वृद्धि और तर्क की वृद्धि के अनुपात की सीमा कहलाती है 
पर 
:
(1.6)
1.4. वेक्टर फ़ंक्शन के पहले व्युत्पन्न का ज्यामितीय और यांत्रिक अर्थ
अदिश तर्क के वेक्टर फ़ंक्शन के पहले व्युत्पन्न का ज्यामितीय अर्थ यह है कि यह व्युत्पन्न होडोग्राफ के लिए स्पर्शरेखीय रूप से निर्देशित एक नया वेक्टर है:
. चलिए दिखाते हैं.
चित्र 2
हम मान लेंगे कि विचाराधीन वेक्टर फ़ंक्शन का होडोग्राफ एक सतत रेखा है जिसमें किसी भी बिंदु पर स्पर्शरेखा होती है।
चलिए तर्क देते हैं टी
वृद्धि, फिर ज्यामितीय रूप से अनुपात 
कुछ वेक्टर है 
, सेकेंट एमएम' पर लेटा हुआ। जब यह वेक्टर घूमता है और वेक्टर में बदल जाता है 
, स्पर्शरेखा पर स्थित है और बढ़ने की ओर निर्देशित हैटी
.
तो वेक्टर
(1.7)
बढ़ते पैरामीटर की दिशा में उन्मुख एक इकाई स्पर्शरेखा वेक्टर होगीटी .
इसलिए, वेक्टर
बिंदु पर वक्र के स्पर्शरेखा दिशा वेक्टर के रूप में लिया जा सकता है), (या 
), और स्पर्शरेखा समीकरण को इस रूप में लिखें:
(1.8)
अगर टी
–
समय और - एक बिंदु का त्रिज्या वेक्टर 
, त्रि-आयामी अंतरिक्ष में घूमना, फिर इसके बारे मेंसंबंध को खंड पर एक बिंदु की औसत गति कहा जाता है [टी;
टी+
टी].
यांत्रिक बोधवेक्टर फ़ंक्शन का पहला व्युत्पन्न यह है कि यह व्युत्पन्न इस समय बिंदु एम की गति का प्रतिनिधित्व करता हैटी
: 
सदिश फलनों के विभेदन के नियम
आइए सदिशों को घटाने और एक सदिश को एक संख्या से विभाजित करने के नियमों का उपयोग करके नियम 1 को सिद्ध करें:
शेष नियमों का प्रमाण नियम 1 और वैक्टर के साथ संचालन के नियमों पर आधारित है।
उदाहरण 1.1: एक वेक्टर फ़ंक्शन दिया गया है।इसका होडोग्राफ बनाएं और एक मनमाने बिंदु पर इसकी स्पर्शरेखा के लिए एक समीकरण बनाएं।
समाधान। किसी भी बिंदु के लिए (
एक्स
,
य
,
जेड
)
होडोग्राफ वेक्टर - हमारे पास कार्य हैं:एक्स
=
लागत
;
य
=
asint
;
जेड
=
बीटी
और इसलिए किसी के लिए भी 
समानता रखती हैएक्स
2
+
य
2
=
ए
2
,
और जेनरेट्रिक्स अक्ष के समानांतर हैआस्ट्रेलिया. यदि पैरामीटर
टी
समय के रूप में व्याख्या की गई, फिर एक वृत्त के चारों ओर समान गति के साथ विमान पर त्रिज्या वेक्टर के अंत का प्रक्षेपणऑक्सी
अक्ष पर इसका प्रक्षेपणआउंस
समान रूप से और सीधी गति से आगे बढ़ेगाबी
.
दूसरे शब्दों में, एक वेक्टर फ़ंक्शन के होडोग्राफ़ बिंदु का अनुप्रयोग विमान पर उसके प्रक्षेपण के घूर्णन के कोण के अनुपात में बढ़ता हैऑक्सी
. इसलिए, वांछित होडोग्राफ का रूप चित्र 3 में दिखाया गया है और इसे हेलिकल लाइन कहा जाता है। होडोग्राफ (पेचदार रेखा) के स्पर्शरेखा को खोजने के लिए, हम वेक्टर फ़ंक्शन का व्युत्पन्न पाते हैं।
समाधान। क्योंकि, तब
परिभाषा 1. वेक्टर जी को स्केलर तर्क टी का एक वेक्टर फ़ंक्शन कहा जाता है यदि अनुमेय मानों की सीमा से स्केलर का प्रत्येक मान वेक्टर आर के एक निश्चित मूल्य से मेल खाता है। हम इसे इस तरह लिखेंगे: यदि वेक्टर आर अदिश तर्क t का एक फलन है तो सदिश r के निर्देशांक x, y, z भी तर्क t के फलन होंगे: अदिश तर्क का सदिश फलन। होडोग्राफ़। एक अदिश तर्क के सदिश फलन की सीमा और निरंतरता। इसके विपरीत, यदि सदिश g के निर्देशांक t% के फलन हैं, तो सदिश g स्वयं t का एक फलन होगा: इस प्रकार, सदिश फलन r(f) को निर्दिष्ट करना है तीन अदिश फलनों y(t), z( t) को निर्दिष्ट करने के बराबर। परिभाषा 2. एक अदिश तर्क के सदिश फलन r(t) का होडोग्राफ उन बिंदुओं का स्थान है जो सदिश r(*) के अंत का वर्णन करता है जब अदिश t बदलता है, जब सदिश r(f) की शुरुआत होती है अंतरिक्ष में एक निश्चित बिंदु O पर रखा गया है (चित्र I)। व्हिस्कर वेक्टर r = g(*) मूवमेंट के लिए होडोग्राफ चित्र। 1 ज्वलन बिंदु स्वयं इस बिंदु का प्रक्षेपवक्र L होगा। इस बिंदु की गति होडोग्राफ v = v(J) कोई अन्य रेखा L\ होगी (चित्र 2)। इसलिए, यदि कोई भौतिक बिंदु एक स्थिर गति |v| के साथ एक वृत्त में घूमता है = const, तो इसका वेग होडोग्राफ भी एक वृत्त है जिसका केंद्र बिंदु 0\ है और त्रिज्या |v| के बराबर है। उदाहरण 1. वेक्टर r = ti + t\ + t\ का एक होडोग्राफ बनाएं। समाधान। 1. यह निर्माण बिंदु दर बिंदु एक तालिका बनाकर किया जा सकता है: चित्र 3 2i आप भी ऐसा ही कर सकते हैं। वेक्टर V के निर्देशांक को x, y, z द्वारा निरूपित करने पर, हमारे पास Hts होगा और इन समीकरणों से कुंजी पैरामीटर 1Y है, हम सतहों y - z = x1 के समीकरण प्राप्त करते हैं, जिसकी प्रतिच्छेदन रेखा L होडोग्राफ का निर्धारण करेगी वेक्टर z() (चित्र 3) का। डी> स्वतंत्र समाधान के लिए कार्य। वैक्टर के होडोग्राफ का निर्माण करें: वेक्टर फ़ंक्शन आर = स्केलर तर्क टी को तर्क टी के मूल्य के कुछ पड़ोस में परिभाषित किया जाए, सिवाय, शायद, समान मूल्य के लिए, एक्सटेंशन 1। स्थिर वेक्टर ए को की सीमा कहा जाता है वेक्टर r(t) पर, यदि किसी e > 0 के लिए b > 0 मौजूद है जैसे कि सभी t φ के लिए स्थिति 11 को संतुष्ट करने के लिए, असमानता कायम है। पारंपरिक विश्लेषण की तरह, limr (0 = A) लिखें। चित्र 4 ज्यामितीय रूप से, इसका मतलब यह है कि वेक्टर) t -* के रूप में वेक्टर की ओर जाता है और लंबाई और दिशा दोनों में (चित्र 4)। परिभाषा 2. वेक्टर a(£) को t -» पर अतिसूक्ष्म कहा जाता है यदि a(£) की t -* पर एक सीमा है और यह सीमा शून्य के बराबर है: एक अदिश तर्क का वेक्टर फ़ंक्शन। होडोग्राफ़। एक अदिश तर्क के सदिश फलन की सीमा और निरंतरता या, जो समान है, किसी भी ई के लिए 6 > 0 मौजूद है जैसे कि सभी टी Ф के लिए शर्त को संतुष्ट करने के लिए, असमानता |ए(£)| उदाहरण 1। दिखाएँ कि वेक्टर t -* 0 के लिए एक असीम रूप से लाल रंग का वेक्टर है। समाधान। हमारे पास यह स्पष्ट है कि यदि किसी e 0 के लिए हम 6 = ~ लेते हैं, तो -0| हम चिन्हित करेंगे | परिभाषा के अनुसार, इसका मतलब है कि a(t) t 0 पर एक अनंत वेक्टर है। 1> r को स्वतंत्र रूप से हल करने के लिए समस्याएं। दिखाएँ कि एक वेक्टर के मापांक की सीमा उसकी सीमा के मापांक के बराबर है यदि बाद की सीमा मौजूद। . साबित करें कि वेक्टर फ़ंक्शन r(*) की एक सीमा A होने के लिए, यह आवश्यक और पर्याप्त है कि r(एक अदिश तर्क के वेक्टर फ़ंक्शन के रूप में दर्शाया जा सकता है। होडोग्राफ। a के वेक्टर फ़ंक्शन की सीमा और निरंतरता अदिश तर्क de a( t) - वेक्टर को t -* t0 के लिए अंतहीन रूप से घुमाएँ। 14. वेक्टर फ़ंक्शन a+ b(*) t = t0 के लिए निरंतर है। क्या इससे यह पता चलता है कि वेक्टर a(t) और b( J) t - से ? 15 के लिए भी सतत हैं। सिद्ध करें कि यदि a( सतत सदिश फलन हैं, तो उनका अदिश गुणनफल (a(*),b(f)) और सदिश गुणनफल |a(f),b(t) )] भी निरंतर हैं।
उदाहरण 2.उदाहरण के लिए, तीन चर वाले एक फ़ंक्शन पर विचार करें एफ(एक्स,पर,जेड), निम्नलिखित सत्य तालिका होना:
मैट्रिक्स विधि
मुद्दा यह है कि बहुत सारे परिवर्तनशील हैं एक्स एनदो भागों में टूट जाता है पर एमऔर जेड एन–एमजैसे कि वेक्टर के सभी संभावित सत्य मान पर एममैट्रिक्स की पंक्तियों और वेक्टर के सभी संभावित सत्य मूल्यों के साथ प्लॉट किए जाते हैं जेड एन - एम- स्तंभों द्वारा. कार्य सत्य मान एफहर सेट पर एन = ( 1 , ..., एम , एम+ 1 ,..., एन) रेखा के प्रतिच्छेदन से बनी कोशिकाओं में रखा जाता है ( 1 , ..., एम) और स्तंभ ( एम+ 1 ,..., एन).
ऊपर चर्चा किए गए उदाहरण 2 में, विभाजन चर के मामले में ( एक्स, वाई, जेड) उपसमुच्चय में ( एक्स) और ( वाई, जेड) मैट्रिक्स फॉर्म लेता है:
|
हाँ,जेड |
|||||
मैट्रिक्स विधि की एक अनिवार्य विशेषता यह है कि चरों का पूरा सेट एक्स एन, पड़ोसी (लंबवत और क्षैतिज दोनों) कोशिकाओं के अनुरूप, एक समन्वय में भिन्न होता है।
पूर्ण बाइनरी ट्री का उपयोग करके निर्दिष्ट करना
विवरण के लिए एन-स्थानीय कार्य एफ( एक्स एन) बाइनरी ट्री की ऊंचाई संपत्ति का उपयोग किया जाता है एन, जिसमें यह तथ्य शामिल है कि इसमें प्रत्येक लटकन शीर्ष वेक्टर मानों के एक निश्चित सेट से एक-से-एक मेल खाता है एक्स एन. तदनुसार, इस लटके हुए शीर्ष को वही सत्य मान दिया जा सकता है जो इस सेट पर फ़ंक्शन का है एफ. एक उदाहरण के रूप में (चित्र 1.3), हम ऊपर चर्चा किए गए टर्नरी फ़ंक्शन के बाइनरी ट्री का उपयोग करके एक कार्य प्रस्तुत करते हैं च =(10110110).
पेड़ के लटकते शीर्षों को निर्दिष्ट संख्याओं की पहली पंक्ति सेट की लेक्सिकोग्राफ़िक संख्या को दर्शाती है, दूसरी - सेट को ही, और तीसरी - उस पर फ़ंक्शन के मान को दर्शाती है।
कार्य का उपयोग करनाएन - आयामी इकाई घनमें एन
शीर्ष के बाद से में एनसभी सेटों के सेट पर एक-से-एक भी मैप किया जा सकता है एक्स एन, वह एन-स्थानीय कार्य एफ(एक्स एन) को घन के संगत शीर्षों पर इसके सत्य मान निर्दिष्ट करके निर्दिष्ट किया जा सकता है में एन . चित्र 1.4 फ़ंक्शन सेटिंग दिखाता है एफ= (10110110) क्यूबा में में 3. सत्य मानों को घन के शीर्षों पर निर्दिष्ट किया गया है।
परिभाषा . तर्क का बीजगणितबूलियन स्थिरांक और चर के एक सेट को उन पर प्रस्तुत तार्किक संयोजकों के साथ नाम दें।
सूत्र कार्य
तर्क बीजगणित कार्यों को विश्लेषणात्मक अभिव्यक्तियों के रूप में निर्दिष्ट किया जा सकता है।
परिभाषा। होने देना एक्स― तार्किक बीजगणित में प्रयुक्त चर और स्थिरांक की वर्णमाला, एफ― 2 से अधिक चरों की संख्या के साथ सभी प्रारंभिक कार्यों और उनके सामान्यीकरणों के लिए नोटेशन का एक सेट।
एक्स, एफ पर फॉर्मूला(तर्क बीजगणित सूत्र) आइए फॉर्म के सभी रिकॉर्ड को कॉल करें:
ए) एक्स,कहाँ एक्स एक्स;
बी) एफ 1 , एफ 1 &एफ 2 ,एफ 1 एफ 2 , एफ 1 एफ 2 , एफ 1 एफ 2 , एफ 1 एफ 2 ,एफ 1 एफ 2 ,एफ 1 एफ 2 , कहाँ एफ 1 , एफ 2 - सूत्र ख़त्म एक्स, एफ;
वी) एच(एफ 1 , … ,एफ एन ), कहाँ एन > 2, एफ 1 ,… ,एफ एन- सूत्र ख़त्म एक्स,एफ, एच ― से सामान्यीकृत थ्रेशोल्ड फ़ंक्शन का निरूपण एफ .
परिभाषा के अनुसार, दो-स्थान के प्रारंभिक कार्यों के लिए संकेतन के इन्फ़िक्स रूप का उपयोग किया जाता है, जिसमें कार्यात्मक प्रतीक को तर्कों के बीच रखा जाता है; निषेध और सामान्यीकृत कार्यों के लिए, संकेतन के उपसर्ग रूप का उपयोग किया जाता है, जिसमें कार्यात्मक प्रतीक तर्कों की सूची से पहले रखा गया है।
उदाहरण 3.
1. भाव एक्स(परजेड); ( एक्स, य, जेड यू) तर्क के बीजगणित के सूत्र हैं, क्योंकि वे ऊपर दी गई परिभाषा को संतुष्ट करते हैं।
2. अभिव्यक्ति एक्स (पर जेड) यह एक तार्किक बीजगणित सूत्र नहीं है क्योंकि ऑपरेशन को गलत तरीके से लागू किया गया था .
परिभाषा। फ़ंक्शन सूत्र एफ द्वारा कार्यान्वित किया गया, चर के मानों को प्रतिस्थापित करके प्राप्त किया गया फ़ंक्शन है एफ।आइए इसे निरूपित करें एफ(एफ).
उदाहरण 4.सूत्र पर विचार करें एफ=xy (एक्सजेड). कार्यान्वित फ़ंक्शन की सत्य तालिका का निर्माण करने के लिए, तार्किक संयोजकों की ताकत को ध्यान में रखते हुए, क्रमिक रूप से तार्किक गुणन करना आवश्यक है। xy, फिर निहितार्थ ( एक्सजेड), फिर परिणामी सत्य मान मॉड्यूल 2 जोड़ें। क्रियाओं का परिणाम तालिका में दिखाया गया है:
|
एक्स जेड | |||||
फ़ंक्शंस का सूत्रबद्ध प्रतिनिधित्व किसी को फ़ंक्शंस के प्राथमिक कई गुणों का मूल्यांकन करने की अनुमति देता है। एक सूत्रीय कार्य से सत्य तालिका में परिवर्तन हमेशा सूत्र में शामिल प्राथमिक कार्यों में सत्य मूल्यों के क्रमिक प्रतिस्थापन द्वारा पूरा किया जा सकता है। विपरीत संक्रमण अस्पष्ट है, क्योंकि एक ही फ़ंक्शन को विभिन्न सूत्रों द्वारा दर्शाया जा सकता है। इस पर अलग से विचार करने की जरूरत है.