dom » Literatura » Stosunek boków i wysokości trójkąta. Podstawowe elementy trójkąta abc. Problem zastosowania twierdzenia Pitagorasa

Stosunek boków i wysokości trójkąta. Podstawowe elementy trójkąta abc. Problem zastosowania twierdzenia Pitagorasa

Przy rozwiązywaniu problemów geometrycznych warto postępować zgodnie z takim algorytmem. Podczas czytania warunków problemu jest to konieczne

Narysuj coś. Rysunek powinien w jak największym stopniu odpowiadać warunkom problemu, dlatego jego głównym zadaniem jest pomoc w znalezieniu rozwiązania
Umieść wszystkie dane z opisu problemu na rysunku
Zapisz wszystkie pojęcia geometryczne, które pojawiają się w zadaniu
Zapamiętaj wszystkie twierdzenia związane z tymi pojęciami
Narysuj na rysunku wszystkie zależności pomiędzy elementami figury geometrycznej, które wynikają z tych twierdzeń

Na przykład, jeśli zadanie zawiera słowa dwusieczna kąta trójkąta, musisz zapamiętać definicję i właściwości dwusiecznej oraz wskazać na rysunku równe lub proporcjonalne odcinki i kąty.

W tym artykule znajdziesz podstawowe właściwości trójkąta, które musisz znać, aby skutecznie rozwiązywać problemy.

TRÓJKĄT.

Pole trójkąta.

1. ,

tutaj - dowolny bok trójkąta, - wysokość obniżona do tej strony.

2. ,

tutaj i są dowolnymi bokami trójkąta i jest kątem między tymi bokami:

3. Wzór Herona:

Oto długości boków trójkąta, to połowa obwodu trójkąta,

4. ,

tutaj jest półobwód trójkąta i jest promień okręgu wpisanego.

Niech będą długościami odcinków stycznych.

Następnie wzór Herona można zapisać w następujący sposób:

6. ,

tutaj - długości boków trójkąta, - promień opisanego koła.

Jeżeli na boku trójkąta weźmiemy punkt dzielący ten bok w stosunku m:n, to odcinek łączący ten punkt z wierzchołkiem przeciwnego kąta dzieli trójkąt na dwa trójkąty, których pola są w stosunku m: n:

Stosunek pól trójkątów podobnych jest równy kwadratowi współczynnika podobieństwa.

Mediana trójkąta

Jest to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.

Mediany trójkąta przecinają się w jednym punkcie i są podzielone przez punkt przecięcia w stosunku 2:1, licząc od wierzchołka.

Punkt przecięcia środkowych trójkąta foremnego dzieli środkową na dwa odcinki, z których mniejszy jest równy promieniowi okręgu wpisanego, a większy jest równy promieniowi opisanego okręgu.

Promień okręgu opisanego jest dwukrotnie większy od promienia okręgu wpisanego: R=2r

Średnia długość dowolny trójkąt

tutaj - środkowa narysowana z boku - długości boków trójkąta.

Dwusieczna trójkąta

Jest to dwusieczna część dowolnego kąta trójkąta łącząca wierzchołek tego kąta z przeciwną stroną.

Dwusieczna trójkąta dzieli bok na odcinki proporcjonalne do sąsiednich boków:

Dwusieczne trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego.

Wszystkie punkty dwusiecznej kąta są w równej odległości od boków kąta.

Wysokość trójkąta

Jest to odcinek prostopadły opadający z wierzchołka trójkąta na przeciwną stronę lub jego kontynuację. W trójkącie rozwartym wysokość wyznaczona z wierzchołka kąta ostrego leży na zewnątrz trójkąta.

Wysokości trójkąta przecinają się w jednym punkcie, który nazywa się ortocentrum trójkąta.

Aby znaleźć wysokość trójkąta narysowany na bok, musisz w dowolny dostępny sposób znaleźć jego pole, a następnie skorzystać ze wzoru:

Środek okręgu opisanego na trójkącie, leży w punkcie przecięcia dwusiecznych prostopadłych poprowadzonych do boków trójkąta.

Promień obwodu trójkąta można znaleźć za pomocą następujących wzorów:

Oto długości boków trójkąta i pole trójkąta.

gdzie jest długością boku trójkąta i jest kątem przeciwnym. (Wzór ten wynika z twierdzenia o sinusie.)

Nierówność trójkąta

Każdy bok trójkąta jest mniejszy od sumy i większy od różnicy pozostałych dwóch.

Suma długości dowolnych dwóch boków jest zawsze większa niż długość trzeciego boku:

Naprzeciwko większego boku znajduje się większy kąt; Naprzeciw większego kąta leży większy bok:

Jeśli , to odwrotnie.

Twierdzenie o sinusach:

Boki trójkąta są proporcjonalne do sinusów przeciwległych kątów:

Twierdzenie cosinus:

Kwadrat boku trójkąta jest równy sumie kwadratów dwóch pozostałych boków, bez podwójnego iloczynu tych boków przez cosinus kąta między nimi:

Trójkąt prostokątny

- To jest trójkąt, którego jeden z kątów ma miarę 90°.

Suma kątów ostrych w trójkącie prostokątnym wynosi 90°.

Przeciwprostokątna to strona leżąca naprzeciwko kąta 90°. Przeciwprostokątna to najdłuższy bok.

Twierdzenie Pitagorasa:

kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg:

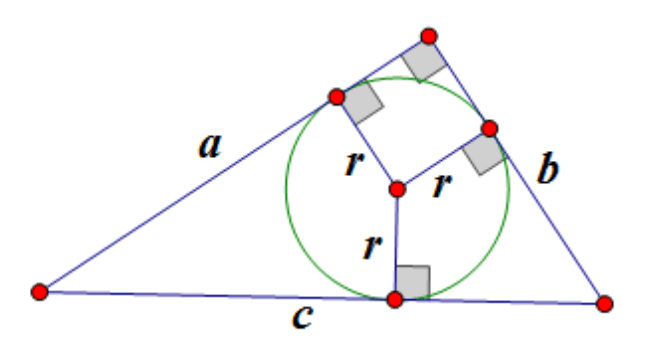
Promień okręgu wpisanego w trójkąt prostokątny jest równy

oto promień okręgu wpisanego, - nogi, - przeciwprostokątna:

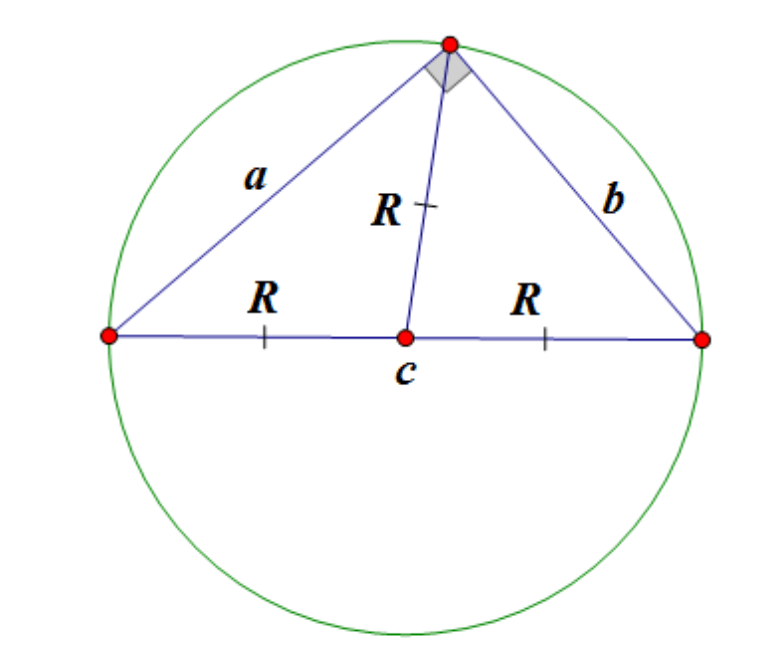
Środek okręgu opisanego na trójkącie prostokątnym leży w środku przeciwprostokątnej:

Mediana trójkąta prostokątnego poprowadzonego do przeciwprostokątnej, jest równe połowie przeciwprostokątnej.

Definicja sinusa, cosinusa, tangensa i cotangensa trójkąta prostokątnego Patrzeć

Stosunek elementów w trójkącie prostokątnym:

Kwadrat wysokości trójkąta prostokątnego narysowanego z wierzchołka kąta prostego jest równy iloczynowi rzutów nóg na przeciwprostokątną:

Kwadrat nogi jest równy iloczynowi przeciwprostokątnej i rzutu nogi na przeciwprostokątną:

Noga leżąca naprzeciwko rogu równy połowie przeciwprostokątnej:

Trójkąt równoramienny.

Dwusieczna trójkąta równoramiennego narysowanego do podstawy to środkowa i wysokość.

W trójkącie równoramiennym kąty przy podstawie są równe.

Kąt wierzchołkowy.

I - boki,

I - kąty u podstawy.

Wysokość, dwusieczna i mediana.

Uwaga! Wysokość, dwusieczna i środkowa narysowana z boku nie pokrywają się.

Zwykły trójkąt

(Lub trójkąt równoboczny ) jest trójkątem, którego wszystkie boki i kąty są sobie równe.

Obszar regularnego trójkąta równy

gdzie jest długość boku trójkąta.

Środek okręgu wpisanego w trójkąt foremny, pokrywa się ze środkiem okręgu opisanego na trójkącie foremnym i leży w punkcie przecięcia środkowych.

Punkt przecięcia środkowych trójkąta foremnego dzieli środkową na dwa odcinki, z których mniejszy jest równy promieniowi okręgu wpisanego, a większy jest równy promieniowi okręgu wpisanego.

Jeśli jeden z kątów trójkąta równoramiennego ma miarę 60°, to trójkąt jest foremny.

Środkowa linia trójkąta

Jest to odcinek łączący środki dwóch boków.

Na rysunku DE jest środkową linią trójkąta ABC.

Linia środkowa trójkąta jest równoległa do trzeciego boku i równa jego połowie: DE||AC, AC=2DE

Kąt zewnętrzny trójkąta

Jest to kąt przylegający do dowolnego kąta trójkąta.

Kąt zewnętrzny trójkąta jest równy sumie dwóch kątów do niego nie przylegających.

Funkcje trygonometryczne kąta zewnętrznego:

Znaki równości trójkątów:

1 . Jeżeli dwa boki i kąt między nimi jednego trójkąta są odpowiednio równe dwóm bokom i kątowi między nimi drugiego trójkąta, to takie trójkąty są przystające.

2 . Jeżeli bok i dwa sąsiednie kąty jednego trójkąta są odpowiednio równe bokowi i dwóm sąsiednim kątom innego trójkąta, to takie trójkąty są przystające.

3 Jeżeli trzy boki jednego trójkąta są odpowiednio równe trzem bokom innego trójkąta, to takie trójkąty są przystające.

Ważny: ponieważ w trójkącie prostokątnym dwa kąty są oczywiście równe, to dla równość dwóch trójkątów prostokątnych wymagana jest równość tylko dwóch elementów: dwóch boków lub boku i kąta ostrego.

Znaki podobieństwa trójkątów:

1 . Jeżeli dwa boki jednego trójkąta są proporcjonalne do dwóch boków innego trójkąta, a kąty między tymi bokami są równe, to te trójkąty są podobne.

2 . Jeśli trzy boki jednego trójkąta są proporcjonalne do trzech boków innego trójkąta, to trójkąty są podobne.

3 . Jeżeli dwa kąty jednego trójkąta są równe dwóm kątom innego trójkąta, to trójkąty są podobne.

Ważny: W podobnych trójkątach podobne boki leżą naprzeciw równych kątów.

Twierdzenie Menelaosa

Niech linia przecina trójkąt, i jest punktem jej przecięcia z boku , jest punktem jego przecięcia z boku i jest punktem jego przecięcia z kontynuacją boku . Następnie

Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.

Jakie dane osobowe zbieramy:

Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres e-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

Gromadzone przez nas dane osobowe pozwalają nam kontaktować się z Tobą w sprawie wyjątkowych ofert, promocji i innych wydarzeń oraz nadchodzących wydarzeń.
Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różnych badań w celu ulepszenia świadczonych przez nas usług i przedstawienia rekomendacji dotyczących naszych usług.
Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.

Ujawnianie informacji osobom trzecim

Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.

Wyjątki:

Jeżeli jest to konieczne – zgodnie z przepisami prawa, procedurą sądową, w postępowaniu sądowym i/lub na podstawie publicznych żądań lub wniosków organów rządowych na terytorium Federacji Rosyjskiej – do ujawnienia Twoich danych osobowych. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub właściwe ze względów bezpieczeństwa, egzekwowania prawa lub innych celów ważnych dla społeczeństwa.
W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.

Szanowanie Twojej prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.

mi za → ⋅ b do → + mi b → ⋅ do za → + mi do → ⋅ ZA b → = 0 (\ displaystyle (\ overrightarrow (EA)) \ cdot (\ overrightarrow (BC)) + (\ overrightarrow (EB)) \ cdot (\ overrightarrow (CA))+(\overrightarrow (EC))\cdot (\overrightarrow (AB))=0)

(Aby udowodnić tożsamość, należy skorzystać ze wzorów

ZA B → = mi b → - mi za → , b do → = mi do → - mi b → , do za → = mi a → - mi do → (\ displaystyle (\ overrightarrow (AB)) = (\ overrightarrow (EB)) - (\ overrightarrow (EA) )),\,(\overrightarrow (BC))=(\overrightarrow (EC))-(\overrightarrow (EB)),\,(\overrightarrow (CA))=(\overrightarrow (EA))-(\overrightarrow (WE)))

Punkt E należy przyjąć jako przecięcie dwóch wysokości trójkąta.)

Ortocentrum izogonalnie sprzężony ze środkiem okrążyć .
Ortocentrum leży na tej samej linii co środek ciężkości, czyli środek okrążyć i środek okręgu dziewięciu punktów (patrz linia prosta Eulera).
Ortocentrum trójkąta ostrego jest środkiem okręgu wpisanego w jego ortotrójkąt.
Środek trójkąta opisanego przez ortocentrum z wierzchołkami w środkach boków danego trójkąta. Ostatni trójkąt nazywany jest trójkątem dopełniającym pierwszy trójkąt.
Ostatnią właściwość można sformułować następująco: Służy środek okręgu opisanego na trójkącie ortocentrum dodatkowy trójkąt.
Punkty, symetryczne ortocentrum trójkąta względem jego boków leżą na okręgu opisanym.
Punkty, symetryczne ortocentrum trójkąty względem środków boków również leżą na opisanym okręgu i pokrywają się z punktami diametralnie przeciwnymi do odpowiednich wierzchołków.
Jeśli O jest zatem środkiem okręgu opisanego ΔABC O H → = O ZA → + O B → + O C → (\ Displaystyle (\ overrightarrow (OH)) = (\ overrightarrow (OA)) + (\ overrightarrow (OB)) + (\ overrightarrow (OC)}) ,
Odległość od wierzchołka trójkąta do ortocentrum jest dwa razy większa niż odległość od środka okręgu opisanego na przeciwną stronę.
Dowolny segment pobrany z ortocentrum przed przecięciem z okręgiem opisanym jest zawsze podzielony na pół przez okrąg Eulera. Ortocentrum jest środkiem jednorodności tych dwóch okręgów.
Twierdzenie Hamiltona. Trzy odcinki linii łączące ortocentrum z wierzchołkami ostrego trójkąta dzielą go na trzy trójkąty mające ten sam okrąg Eulera (okrąg złożony z dziewięciu punktów), co pierwotny ostry trójkąt.
Wnioski z twierdzenia Hamiltona:
- Trzy odcinki proste łączące ortocentrum z wierzchołkami ostrego trójkąta dzielą go na trzy części Trójkąt Hamiltona mające równe promienie opisanych okręgów.
- Promienie opisanych okręgów trzech Trójkąty Hamiltona równy promieniowi okręgu opisanego na pierwotnym ostrym trójkącie.
W ostrym trójkącie ortocentrum leży wewnątrz trójkąta; pod kątem rozwartym - na zewnątrz trójkąta; w prostokątnym - w wierzchołku kąta prostego.

Własności wysokości trójkąta równoramiennego

Jeśli dwie wysokości w trójkącie są równe, to trójkąt jest równoramienny (twierdzenie Steinera-Lemusa), a trzecia wysokość jest zarówno medianą, jak i dwusieczną kąta, z którego się wyłania.
Odwrotna sytuacja jest również prawdziwa: w trójkącie równoramiennym dwie wysokości są równe, a trzecia wysokość jest zarówno środkową, jak i dwusieczną.
Trójkąt równoboczny ma wszystkie trzy wysokości równe.

Własności podstaw wysokości trójkąta

Powody wysokości tworzą tak zwany ortotrójkąt, który ma swoje własne właściwości.
Okrąg opisany na ortotrójkącie to okrąg Eulera. Okrąg ten zawiera również trzy środki boków trójkąta i trzy punkty środkowe trzech odcinków łączących ortocentrum z wierzchołkami trójkąta.
Inne sformułowanie ostatniej właściwości:
- Twierdzenie Eulera dla okręgu dziewięciu punktów. Powody trzy wysokości dowolny trójkąt, środki jego trzech boków ( podstawy jego wnętrzaśrodkowe) i środki trzech odcinków łączących ich wierzchołki z ortocentrum, wszystkie leżą na tym samym okręgu (na okrąg z dziewięcioma punktami).
Twierdzenie. W dowolnym trójkącie segment się łączy fusy dwa wysokości trójkąt, odcina trójkąt podobny do podanego.
Twierdzenie. W trójkącie segment się łączy fusy dwa wysokości trójkąty leżące po dwóch stronach antyrównoległe osobie trzeciej, z którą nie ma wspólnej płaszczyzny porozumienia. Okrąg zawsze można poprowadzić przez jego dwa końce, a także przez dwa wierzchołki trzeciego wspomnianego boku.

Inne właściwości wysokości trójkątów

Własności minimalnej wysokości trójkąta

Minimalna wysokość trójkąta ma wiele ekstremalnych właściwości. Na przykład:

Minimalny rzut ortogonalny trójkąta na linie leżące w płaszczyźnie trójkąta ma długość równą najmniejszej z jego wysokości.
Minimalne proste cięcie w płaszczyźnie, przez które można przeciągnąć sztywną trójkątną płytę, musi mieć długość równą najmniejszej z wysokości tej płyty.
Przy ciągłym ruchu dwóch punktów wzdłuż obwodu trójkąta ku sobie, maksymalna odległość między nimi podczas ruchu od pierwszego spotkania do drugiego nie może być mniejsza niż długość najmniejszej wysokości trójkąta.
Minimalna wysokość w trójkącie zawsze mieści się w tym trójkącie.

Podstawowe relacje

godz za = b grzech ⁡ γ = do grzech ⁡ β , (\ Displaystyle h_ (a) = b \ sin \ gamma = c \ sin \ beta,)
godz za = 2 S za , (\ Displaystyle h_ (a) = (\ Frac (2S) (a)),) Gdzie S (\ displaystyle S)- pole trójkąta, za (\ displaystyle a)- długość boku trójkąta, o który obniżona jest wysokość.
godz za 2 = 1 2 (b 2 + do 2 - 1 2 (za 2 + (b 2 - do 2) 2 za 2)) (\ Displaystyle h_ (a) ^ (2) = (\ Frac (1) (2 ))(b^(2)+c^(2)-(\frac (1)(2))(a^(2)+(\frac ((b^(2)-c^(2))^ (2))(a^(2))))))
godz za = b do 2 R , (\ Displaystyle h_ (a) = (\ Frac (bc) (2R)),) Gdzie b do (\ displaystyle bc)- produkt boków, R - (\ displaystyle R-) promień okręgu opisanego
godz za: godz b: godz do = 1 za: 1 b: 1 do = b do: za do: za b (\ displaystyle h_ (a): h_ (b): h_ (c) = (\ Frac (1) (a)): ( \frac (1)(b)):(\frac (1)(c))=bc:ac:ab)
1 godz za + 1 godz b + 1 godz do = 1 r (\ Displaystyle (\ Frac (1) (h_ (a))) + (\ Frac (1) (h_ (b))) + (\ Frac (1) (h_ (c)))=(\frac (1)(r))), Gdzie r (\ displaystyle r)- promień okręgu wpisanego.
S = 1 (1 godz. za + 1 godz. b + 1 godz. do) ⋅ (1 godz. za + 1 godz. b - 1 godz. do) ⋅ (1 godz. za + 1 godz. do - 1 godz. b) ⋅ (1 godz. b + 1 godz. do - 1 godz. za) (\ displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), Gdzie S (\ displaystyle S)- pole trójkąta.
za = 2 godz. za ⋅ (1 godz. za + 1 godz. b + 1 godz. do) ⋅ (1 godz. za + 1 godz. b - 1 godz. do) ⋅ (1 godz. za + 1 godz. do - 1 godz. b) ⋅ (1 godz. b + 1 godz. do - 1 godz. a) (\ displaystyle a = (\ Frac (2) (h_ (a) (\ cdot) (\ sqrt ({{\ Frac (1) (h_ (a))) + (\ Frac (1) (h_ (b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c)))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (A))))))))), za (\ displaystyle a)- bok trójkąta, do którego schodzi wysokość h za (\ displaystyle h_ (a)).
Wysokość trójkąta równoramiennego obniżonego do podstawy: godz do = 1 2 4 za 2 - do 2 , (\ Displaystyle h_ (c) = (\ Frac (1) (2)) (\ sqrt (4a ^ (2) -c ^ (2))),}

Gdzie do (\ displaystyle c)- baza, za (\ displaystyle a)- strona.

Twierdzenie o wysokości trójkąta prostokątnego

Jeśli wysokość w trójkącie prostokątnym ZA B C (\ displaystyle ABC) długość h (\ displaystyle h) narysowany z wierzchołka kąta prostego, dzieli przeciwprostokątną przez długość do (\ displaystyle c) na segmenty m (\ displaystyle m) I n (\ displaystyle n), odpowiadający nogom b (\ displaystyle b) I za (\ displaystyle a), to prawdziwe są następujące równości.

Trójkąt) lub przejść na zewnątrz trójkąta przy trójkącie rozwartym.

Encyklopedyczny YouTube

1 / 5

✪ WYSOKOŚĆ ŚREDNIA Dwusieczna trójkąta Stopień 7

✪ dwusieczna, środkowa, wysokość trójkąta. Geometria w klasie 7

✪ Klasa 7, lekcja 17, Mediany, dwusieczne i wysokości trójkąta

✪ Mediana, dwusieczna, wysokość trójkąta | Geometria

✪ Jak znaleźć długość dwusiecznej, medianę i wysokość? | Kujon ze mną #031 | Borys Truszyn

Napisy na filmie obcojęzycznym

Właściwości punktu przecięcia trzech wysokości trójkąta (ortocentrum)

(Aby udowodnić tożsamość, należy skorzystać ze wzorów

Punkt E należy przyjąć jako przecięcie dwóch wysokości trójkąta.)

Ortocentrum izogonalnie sprzężony ze środkiem opisany okrąg .
Ortocentrum leży na tej samej linii co środek ciężkości, czyli środek okrążyć i środek okręgu składającego się z dziewięciu punktów (patrz linia prosta Eulera).
Ortocentrum trójkąta ostrego jest środkiem okręgu wpisanego w jego ortotrójkąt.
Środek trójkąta opisanego przez ortocentrum z wierzchołkami w środkach boków danego trójkąta. Ostatni trójkąt nazywany jest trójkątem dopełniającym pierwszy trójkąt.
Ostatnią właściwość można sformułować następująco: Służy środek okręgu opisanego na trójkącie ortocentrum dodatkowy trójkąt.
Punkty, symetryczne ortocentrum trójkąta względem jego boków leżą na okręgu opisanym.
Punkty, symetryczne ortocentrum trójkąty względem środków boków również leżą na opisanym okręgu i pokrywają się z punktami diametralnie przeciwnymi do odpowiednich wierzchołków.
Jeżeli O jest środkiem okręgu opisanego ΔABC, to O H → = O ZA → + O B → + O C → (\ Displaystyle (\ overrightarrow (OH)) = (\ overrightarrow (OA)) + (\ overrightarrow (OB)) + (\ overrightarrow (OC)}) ,
Odległość od wierzchołka trójkąta do ortocentrum jest dwa razy większa niż odległość od środka okręgu opisanego na przeciwną stronę.
Dowolny segment pobrany z ortocentrum Przed przecięciem z okręgiem opisanym jest on zawsze podzielony na pół przez okrąg Eulera. Ortocentrum jest środkiem jednorodności tych dwóch okręgów.
Twierdzenie Hamiltona. Trzy proste odcinki łączące ortocentrum z wierzchołkami ostrego trójkąta dzielą go na trzy trójkąty mające ten sam okrąg Eulera (okrąg złożony z dziewięciu punktów), co pierwotny ostry trójkąt.
Wnioski z twierdzenia Hamiltona:
- Trzy odcinki proste łączące ortocentrum z wierzchołkami ostrego trójkąta dzielą go na trzy części Trójkąt Hamiltona mające równe promienie opisanych okręgów.
- Promienie opisanych okręgów trzech Trójkąty Hamiltona równy promieniowi okręgu opisanego na pierwotnym ostrym trójkącie.
W ostrym trójkącie ortocentrum leży wewnątrz trójkąta; pod kątem rozwartym - na zewnątrz trójkąta; w prostokątnym - w wierzchołku kąta prostego.

Własności wysokości trójkąta równoramiennego

Jeśli dwie wysokości w trójkącie są równe, to trójkąt jest równoramienny (twierdzenie Steinera-Lemusa), a trzecia wysokość jest zarówno medianą, jak i dwusieczną kąta, z którego się wyłania.
Odwrotna sytuacja jest również prawdziwa: w trójkącie równoramiennym dwie wysokości są równe, a trzecia wysokość jest zarówno środkową, jak i dwusieczną.
Trójkąt równoboczny ma wszystkie trzy wysokości równe.

Własności podstaw wysokości trójkąta

Powody wysokości tworzą tak zwany ortotrójkąt, który ma swoje własne właściwości.
Okrąg opisany na ortotrójkącie to okrąg Eulera. Okrąg ten zawiera również trzy środki boków trójkąta i trzy punkty środkowe trzech odcinków łączących ortocentrum z wierzchołkami trójkąta.
Inne sformułowanie ostatniej właściwości:
- Twierdzenie Eulera dla okręgu dziewięciu punktów. Powody trzy wysokości dowolny trójkąt, środki jego trzech boków ( podstawy jego wnętrzaśrodkowe) i środki trzech odcinków łączących ich wierzchołki z ortocentrum, wszystkie leżą na tym samym okręgu (na okrąg z dziewięcioma punktami).
Twierdzenie. W dowolnym trójkącie segment się łączy fusy dwa wysokości trójkąt, odcina trójkąt podobny do podanego.
Twierdzenie. W trójkącie segment się łączy fusy dwa wysokości trójkąty leżące po dwóch stronach antyrównoległe osobie trzeciej, z którą nie ma wspólnej płaszczyzny porozumienia. Okrąg zawsze można poprowadzić przez jego dwa końce, a także przez dwa wierzchołki trzeciego wspomnianego boku.

Inne właściwości wysokości trójkątów

Jeśli trójkąt wszechstronny (różnoboczny), potem to wewnętrzny dwusieczna narysowana z dowolnego wierzchołka leży pomiędzy wewnętrzny mediana i wysokość narysowane z tego samego wierzchołka.
Wysokość trójkąta jest izogonalnie sprzężona ze średnicą (promieniem) opisany okrąg, narysowane z tego samego wierzchołka.
W ostrym trójkącie są dwa wysokości wytnij z niego podobne trójkąty.
W trójkącie prostokątnym wysokość, narysowany z wierzchołka kąta prostego, dzieli go na dwa trójkąty podobne do pierwotnego.

Własności minimalnej wysokości trójkąta

Minimalna wysokość trójkąta ma wiele ekstremalnych właściwości. Na przykład:

Minimalny rzut ortogonalny trójkąta na linie leżące w płaszczyźnie trójkąta ma długość równą najmniejszej z jego wysokości.
Minimalne proste cięcie w płaszczyźnie, przez które można przeciągnąć sztywną trójkątną płytę, musi mieć długość równą najmniejszej z wysokości tej płyty.
Przy ciągłym ruchu dwóch punktów wzdłuż obwodu trójkąta ku sobie, maksymalna odległość między nimi podczas ruchu od pierwszego spotkania do drugiego nie może być mniejsza niż długość najmniejszej wysokości trójkąta.
Minimalna wysokość w trójkącie zawsze mieści się w tym trójkącie.

Podstawowe relacje

godz za = b ⋅ grzech ⁡ γ = do ⋅ grzech ⁡ β , (\ Displaystyle h_ (a) = b (\ cdot) \ sin \ gamma = c (\ cdot) \ sin \ beta,)
godz za = 2 ⋅ S za , (\ Displaystyle h_ (a) = (\ Frac (2 (\ cdot) S) (a)),} Gdzie S (\ displaystyle S)- pole trójkąta, za (\ displaystyle a)- długość boku trójkąta, o który obniżona jest wysokość.
godz za = b ⋅ do 2 ⋅ R , (\ Displaystyle h_ (a) = (\ Frac (b (\ cdot) c) (2 (\ cdot) R)),} Gdzie b ⋅ do (\ Displaystyle b (\ cdot) c)- produkt boków, R - (\ displaystyle R-) promień okręgu opisanego
godz za: godz b: godz do = 1 za: 1 b: 1 do = (b ⋅ do): (za ⋅ do): (za ⋅ b) . (\ Displaystyle h_ (a): h_ (b): h_ (c) = (\ Frac (1) (a)): (\ Frac (1) (b)): (\ Frac (1) (c)) =(b(\cdot )c):(a(\cdot )c):(a(\cdot )b).)
1 godz za + 1 godz b + 1 godz do = 1 r (\ Displaystyle (\ Frac (1) (h_ (a))) + (\ Frac (1) (h_ (b))) + (\ Frac (1) (h_ (c)))=(\frac (1)(r))), Gdzie r (\ displaystyle r)- promień okręgu wpisanego.
S = 1 (1 godz. za + 1 godz. b + 1 godz. do) ⋅ (1 godz. za + 1 godz. b - 1 godz. do) ⋅ (1 godz. za + 1 godz. do - 1 godz. b) ⋅ (1 godz. b + 1 godz. do - 1 godz. za) (\ displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), Gdzie S (\ displaystyle S)- pole trójkąta.
za = 2 godz. za ⋅ (1 godz. za + 1 godz. b + 1 godz. do) ⋅ (1 godz. za + 1 godz. b - 1 godz. do) ⋅ (1 godz. za + 1 godz. do - 1 godz. b) ⋅ (1 godz. b + 1 godz. do - 1 godz. a) (\ displaystyle a = (\ Frac (2) (h_ (a) (\ cdot) (\ sqrt ({{\ Frac (1) (h_ (a))) + (\ Frac (1) (h_ (b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c)))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (A))))))))), za (\ displaystyle a)- bok trójkąta, do którego schodzi wysokość h za (\ displaystyle h_ (a)).
Wysokość trójkąta równoramiennego obniżonego do podstawy: godz do = 1 2 ⋅ 4 za 2 - do 2 , (\ Displaystyle h_ (c) = (\ Frac (1) (2)) (\ cdot) (\ sqrt (4a ^ (2) -c ^ (2)) ))

Gdzie do (\ displaystyle c)- baza, za (\ displaystyle a)- strona.

Twierdzenie o wysokości trójkąta prostokątnego

Jeśli wysokość w trójkącie prostokątnym ABC ma długość h (\ displaystyle h) narysowany z wierzchołka kąta prostego, dzieli przeciwprostokątną przez długość do (\ displaystyle c) na segmenty m (\ displaystyle m) I n (\ displaystyle n), odpowiadający nogom b (\ displaystyle b) I za (\ displaystyle a), to prawdziwe są następujące równości.

Kurs wideo „Zdobądź piątkę” obejmuje wszystkie tematy niezbędne do pomyślnego zdania jednolitego egzaminu państwowego z matematyki z wynikiem 60–65 punktów. Całkowicie wszystkie zadania 1-13 z egzaminu państwowego Profile Unified z matematyki. Nadaje się również do zdania podstawowego jednolitego egzaminu państwowego z matematyki. Jeśli chcesz zdać Unified State Exam z 90-100 punktami, musisz rozwiązać część 1 w 30 minut i bez błędów!

Kurs przygotowawczy do Jednolitego Egzaminu Państwowego dla klas 10-11, a także dla nauczycieli. Wszystko, czego potrzebujesz, aby rozwiązać część 1 egzaminu państwowego Unified State Exam z matematyki (pierwsze 12 zadań) i zadanie 13 (trygonometria). A to ponad 70 punktów na egzaminie Unified State Exam i ani 100-punktowy student, ani student nauk humanistycznych nie mogą się bez nich obejść.

Cała niezbędna teoria. Szybkie rozwiązania, pułapki i tajemnice Unified State Exam. Przeanalizowano wszystkie aktualne zadania części 1 z Banku Zadań FIPI. Kurs w pełni odpowiada wymogom Unified State Exam 2018.

Kurs zawiera 5 dużych tematów, każdy po 2,5 godziny. Każdy temat jest podany od podstaw, prosto i przejrzyście.

Setki zadań z egzaminu Unified State Exam. Zadania tekstowe i teoria prawdopodobieństwa. Proste i łatwe do zapamiętania algorytmy rozwiązywania problemów. Geometria. Teoria, materiały referencyjne, analiza wszystkich typów zadań Unified State Examation. Stereometria. Podstępne rozwiązania, przydatne ściągawki, rozwój wyobraźni przestrzennej. Trygonometria od podstaw do zadania 13. Zrozumienie zamiast wkuwania. Jasne wyjaśnienia skomplikowanych pojęć. Algebra. Pierwiastki, potęgi i logarytmy, funkcja i pochodna. Podstawa do rozwiązywania złożonych problemów części 2 jednolitego egzaminu państwowego.

Udział: